练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    直线y＝mx(m＞0)与抛物线y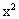＝－2x＋2交于A，B两点，在线段AB上有动点P，使|OA|，|OP|，|OB|的倒数成等差数列，求P点的轨迹方程．

    答案：
    解析：

    　　解 设直线y＝mx的参数方程为(t为参数，tanα＝m)．∵m＞0，∴α为锐角．将代入y＝－2x＋2并整理得α－(2cosα＋sinα)t＋2＝0(*)．设(*)的两根为．动点P在直线上对应的参数为t，由得．∵A，P，B三点在原点O的上方，∴＞0，t＞0，＞0，，则t．设P(x，y)，则①×2＋②得2x＋y＝4即2x＋y－4＝0．又(*)的判别式Δ＝4＋4sinαcosα＋－α＞0，又α为锐角，化得tanα＞－2＋2．∴，∴0＜x＜．∴P点的轨迹方程是2x＋y－4＝0(0＜x＜)．

    　　说明 用直线的参数方程中参数的几何意义应易获得线段间关系的数学表达式．凡用韦达定理寻求关系式，一般要考虑Δ＞0．本题中P点轨迹的范围往往被误以为是直线2x＋y－4＝0在抛物线内部的部分．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：江苏省南通市海门市2008届高三第一次诊断性考试数学(理) 题型：022

    直线l：y＝mx(m＞0)与抛物线y＝x2＋2ax(其中a＜0且a为常数)所围成的图形的面积为，则m＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设点M（x，y）到直线x＝4的距离与它到定点（1，0）的距离之比为2，并记点M的轨迹曲线为C．

    　 （Ⅰ）求曲线C的方程；

    （Ⅱ）设过定点（0，2）的直线l与曲线C交于不同的两点E，F，且∠EOF＝90°（其中O为坐标原点），求直线l的斜率k的值；

    　 （Ⅲ）设A（2，0），B（0，）是曲线C的两个顶点，直线y＝mx（m>0）与线段AB相交于点D，与椭圆相交于E，F两点．求四边形AEBF面积的最大值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知两点M和N分别在直线y＝mx和y＝－mx(m＞0)上运动，且|MN|＝2，动点P满足：2＝＋ (O为坐标原点)，点P的轨迹记为曲线C.

    (1)求曲线C的方程，并讨论曲线C的类型；

    (2)过点(0,1)作直线l与曲线C交于不同的两点A、B，若对于任意m＞1，都有∠AOB为锐角，求直线l的斜率k的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知平面区域Ω＝{(x，y)|}，直线y＝mx＋2m和曲线y＝有两个不同的交点，它们围成的平面区域为M，向区域Ω上随机投一点A，点A落在区域M内的概率为P(M)，若0≤m≤1，则P(M)的取值范围为(　　)

    查看答案和解析>>

    同步练习册答案