练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．RAND（0，1）表示生成一个在（0，1）内的随机数（实数），若x=RAND（0，1），y=RAND（0，1），则x2+y2＜1的概率为（　　）
    A．$\frac{π}{4}$B．$1-\frac{π}{4}$C．$\frac{π}{8}$D．$1-\frac{π}{8}$

    分析 直接由题意作出图形，利用面积比得答案．

    解答 解：设事件A：x2+y2＜1，
    作出图形如图：

    ∴满足x2+y2＜1的概率为P=$\frac{\frac{1}{4}×π×{1}^{2}}{1×1}=\frac{π}{4}$．
    故选：A．

    点评 本题考查了几何概型的概率求法，关键是对随机数的理解，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    14．谷志伟，简书两位老师下棋，简老师获胜的概率是40%，谷老师不胜的概率为60%，则两位老师下成和棋的概率为（　　）
    A．10%B．30%C．20%D．50%

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．设f（x）=$\left\{\begin{array}{l}{lo{g}_{4}x-1，x＞0}\\{{2}^{x}-x+\frac{1}{3}{a}^{3}，x≤0}\end{array}\right.$，若f（f（4））=$\frac{11}{3}$，则a=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数$f（x）=\frac{{m•{4^x}+1}}{2^x}$是偶函数．
    （1）求实数m的值；
    （2）若关于x的不等式2k•f（x）＞3k2+1在（-∞，0）上恒成立，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知a＞2，b＞2，直线$y=-\frac{b}{a}x+b$与曲线（x-1）2+（y-1）2=1只有一个公共点，则ab的取值范围为（　　）
    A．$（4，6+4\sqrt{2}）$B．$（4，6+4\sqrt{2}]$C．$[6+4\sqrt{2}，+∞）$D．$（6+4\sqrt{2}，+∞）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知正四面体ABCD的四个顶点都在球心为O的球面上，点P为棱BC的中点，$BC=6\sqrt{2}$，过点P作球O的截面，则截面面积的最小值为18π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，椭圆C和抛物线y2=x交于M，N两点，且直线MN恰好通过椭圆C的右焦点．
    （I）求椭圆C的标准方程；
    （II）A为椭圆的右顶点，经过原点的直线和椭圆C交于B，D两点，设直线AB与AD的斜率分别为k1，k2．问k1•k2是否为定值？若为定值，请求出；否则，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

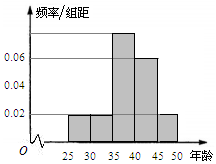    13．某单位280名员工参加“我爱阅读”活动，他们的年龄在25岁至50岁之间，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50），得到的频率分布直方图如图所示．
    （ I）现要从年龄低于40岁的员工中用分层抽样的方法抽取12人，则年龄在第1，2，3组的员工人数分别是多少？
    （ II）为了交流读书心得，现从上述12人中再随机抽取3人发言，设3人中年龄在[35，40）的人数为ξ，求ξ的数学期望；
    （ III）为了估计该单位员工的阅读倾向，现对从该单位所有员工中按性别比例抽取的40人做“是否喜欢阅读国学类书籍”进行调查，调查结果如下表所示：（单位：人）
    喜欢阅读国学类 不喜欢阅读国学类 合计
     男 14 4 18
     女 8 14 22
     合计 22 18 40
    根据表中数据，我们能否有99%的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系？
    附：${K^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$，其中n=a+b+c+d
    P（K2≥k0）0.050.0250.0100.0050.001
    k03.8415.0246.6357.87910.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

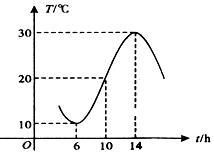    14．如图所示，某地一天6～14时的温度变化曲线近似满足函数y=Asin（ωx+ϕ）+b，则这段曲线的函数解析式可以为（　　）
    A．$y=10sin（\frac{π}{8}x+\frac{3π}{4}）+20$，x∈[6，14]B．$y=10sin（\frac{π}{8}x+\frac{5π}{4}）+20$，x∈[6，14]
    C．$y=10sin（\frac{π}{8}x-\frac{3π}{4}）+20$，x∈[6，14]D．$y=10sin（\frac{π}{8}x+\frac{5π}{8}）+20$，x∈[6，14]

    查看答案和解析>>

    同步练习册答案