
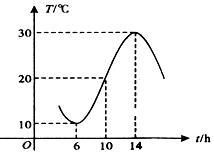
 如图所示,某地一天6~14时的温度变化曲线近似满足函数y=Asin(ωx+ϕ)+b,则这段曲线的函数解析式可以为( )
如图所示,某地一天6~14时的温度变化曲线近似满足函数y=Asin(ωx+ϕ)+b,则这段曲线的函数解析式可以为( )| A. | $y=10sin(\frac{π}{8}x+\frac{3π}{4})+20$,x∈[6,14] | B. | $y=10sin(\frac{π}{8}x+\frac{5π}{4})+20$,x∈[6,14] | ||
| C. | $y=10sin(\frac{π}{8}x-\frac{3π}{4})+20$,x∈[6,14] | D. | $y=10sin(\frac{π}{8}x+\frac{5π}{8})+20$,x∈[6,14] |
分析 由函数的图象的顶点坐标求出A和b,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
解答 解:根据函数y=Asin(ωx+ϕ)+b的图象,可得b=$\frac{30+10}{2}$=20,A=$\frac{30-10}{2}$=10,$\frac{T}{2}$=$\frac{π}{ω}$=14-6=8,∴ω=$\frac{π}{8}$,
再根据五点法作图可得$\frac{π}{8}$•10+φ=2π,∴φ=$\frac{3π}{4}$,∴函数的解析式为y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,
故选:A.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A和b,由周期求出ω,由五点法作图求出φ的值,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $1-\frac{π}{4}$ | C. | $\frac{π}{8}$ | D. | $1-\frac{π}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
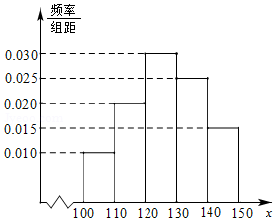 扶贫工作组帮助某村成立菠萝加工厂,加工菠萝罐头销售.在一个生产季内,销售1吨菠萝罐头可获利0.5万元,未销售的每吨亏损0.1万元.根据历年统计数据得到在生产季内菠萝罐头市场需求量x(100≤x≤150,单位:吨)的频率分布直方图如图.已知该厂在下一生产季计划生产130吨菠萝罐头.
扶贫工作组帮助某村成立菠萝加工厂,加工菠萝罐头销售.在一个生产季内,销售1吨菠萝罐头可获利0.5万元,未销售的每吨亏损0.1万元.根据历年统计数据得到在生产季内菠萝罐头市场需求量x(100≤x≤150,单位:吨)的频率分布直方图如图.已知该厂在下一生产季计划生产130吨菠萝罐头.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com