
分析 (1)利用绝对值不等式的意义,通过x的讨论 去掉绝对值符号,求解不等式的解集即可.
(2)利用分析法的证明方法,推出不等式成立的充分条件即可.
解答 解:(1)当$x≤-\frac{3}{2}$时,-x+5+2x+3≥1,解得x≤-7,∴$-7≤x≤-\frac{3}{2}$;
当$-\frac{3}{2}<x<5$时,-x+5-2x-3≥1,解得$x≤\frac{1}{3}$,∴$-\frac{3}{2}<x≤\frac{1}{3}$;
当x≥5时,x-5-(2x+3)≥1,解得x≤-9,舍去.
综上,$-7≤x≤\frac{1}{3}$.故原不等式的解集为$\{x|-7≤x≤\frac{1}{3}\}$.
(2)证明:要证$\sqrt{a}+\sqrt{b}≤1$,只需证$a+b+2\sqrt{ab}≤1$,即证$2\sqrt{ab}≤\frac{1}{2}$,即证$\sqrt{ab}≤\frac{1}{4}$,
而$a+b=\frac{1}{2}≥2\sqrt{ab}$,所以$\sqrt{ab}≤\frac{1}{4}$成立,所以原不等式成立.
点评 本题考查绝对值不等式的解法,不等式的证明,考查计算能力.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
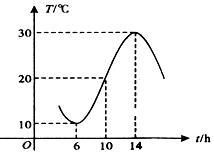 如图所示,某地一天6~14时的温度变化曲线近似满足函数y=Asin(ωx+ϕ)+b,则这段曲线的函数解析式可以为( )
如图所示,某地一天6~14时的温度变化曲线近似满足函数y=Asin(ωx+ϕ)+b,则这段曲线的函数解析式可以为( )| A. | $y=10sin(\frac{π}{8}x+\frac{3π}{4})+20$,x∈[6,14] | B. | $y=10sin(\frac{π}{8}x+\frac{5π}{4})+20$,x∈[6,14] | ||
| C. | $y=10sin(\frac{π}{8}x-\frac{3π}{4})+20$,x∈[6,14] | D. | $y=10sin(\frac{π}{8}x+\frac{5π}{8})+20$,x∈[6,14] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4} | B. | {2,3,4} | C. | {3} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{5}{4}+ln2,2})$ | B. | $[{2-ln2,\frac{5}{4}+ln2})$ | C. | $({\frac{5}{4}+ln2,2-ln2}]$ | D. | (2-ln2,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com