
分析 由x-1>0,f(x)=(x-1)+$\frac{m}{x-1}$+1,运用基本不等式可得最小值,解方程可得p的值.
解答 解:由x>1可得x-1>0,即有f(x)=(x-1)+$\frac{m}{x-1}$+1
≥2$\sqrt{(x-1)•\frac{m}{x-1}}$+1=2$\sqrt{m}$+1,
当且仅当x-1=$\frac{m}{x-1}$,即x=1+$\sqrt{m}$处取得最小值,且为1+2$\sqrt{m}$,
由题意可得1+2$\sqrt{m}$=3,解得m=1.
故答案为:1.
点评 本题考查函数的最值的求法,注意运用基本不等式,考查运算能力,属于基础题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
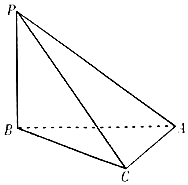 如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=$\sqrt{3}CA=\sqrt{3}$,则三棱锥P-ABC的外接球体积为$\frac{4π}{3}$.
如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=$\sqrt{3}CA=\sqrt{3}$,则三棱锥P-ABC的外接球体积为$\frac{4π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年宣传费x(万元) | 38 | 48 | 58 | 68 | 78 | 88 |
| 年销售量y(吨) | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
| $\sum_{i=1}^{6}$(lnxi•lnyi) | $\sum_{i=1}^{6}$(lnxi) | $\sum_{i=1}^{6}$(lnyi) | $\sum_{i=1}^{6}$(lnxi)2 |
| 75.3 | 24.6 | 18.3 | 101.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,6] | B. | [-3,5] | C. | [2,6] | D. | [3,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,+∞) | B. | (3,+∞) | C. | (-∞,-1) | D. | (1,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com