
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年宣传费x(万元) | 38 | 48 | 58 | 68 | 78 | 88 |
| 年销售量y(吨) | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
| $\sum_{i=1}^{6}$(lnxi•lnyi) | $\sum_{i=1}^{6}$(lnxi) | $\sum_{i=1}^{6}$(lnyi) | $\sum_{i=1}^{6}$(lnxi)2 |
| 75.3 | 24.6 | 18.3 | 101.4 |
分析 (Ⅰ)对y=a•bx,(a>0,b>0)两边取对数,得lny=b•lnx+lna,令μi=lnxi,vi=lnyi,得v=b•μ+lna,利用最小二乘法求出得a=e,由此能求出y关于x的回归方程.
(Ⅱ)由题意得到ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列和E(ξ).
解答 解:(Ⅰ)对y=a•bx,(a>0,b>0)两边取对数,得lny=b•lnx+lna,
令μi=lnxi,vi=lnyi,得v=b•μ+lna,
由题所给的数据得:
$\overline{μ}=\frac{24.6}{6}=4.1$,$\overline{v}$=$\frac{18.3}{6}$=3.05,
$\sum_{i=1}^{6}({μ}_{i}•{v}_{i})=\sum_{i=1}^{6}(ln{x}_{i}•ln{y}_{i})$=75.3,
$\sum_{i=1}^{6}(ln{x}_{i})^{2}=101.4$,
∴$\widehat{β}$=$\frac{\sum_{i=1}^{n}({μ}_{i}•{v}_{i})-n(\overline{μ}•\overline{v})}{\sum_{i=1}^{n}{{μ}_{i}}^{2}-n(\overline{μ})^{2}}$,$\widehat{α}=\overline{v}-\widehat{β}•\overline{μ}$,
$lna=\overline{v}-b•\overline{μ}$=3.05-$\frac{1}{2}×4.1$=1,得a=e,
∴y关于x的回归方程为$y=e•\sqrt{x}$.
(Ⅱ)由(Ⅰ)中所求回归方程,得$\frac{y}{x}=\frac{e}{\sqrt{x}}∈(\frac{e}{9},\frac{e}{7})$,则x∈(49,81),
∴x=58,68,78,∴ξ的可能取值为0,1,2,3,
P(ξ=0)=$\frac{{C}_{3}^{0}{C}_{3}^{3}}{{C}_{6}^{3}}=\frac{1}{20}$,
P(ξ=1)=$\frac{{C}_{3}^{1}{C}_{3}^{2}}{{C}_{6}^{3}}$=$\frac{9}{20}$,
P(ξ=2)=$\frac{{C}_{3}^{2}{C}_{3}^{1}}{{C}_{6}^{3}}$=$\frac{9}{20}$,
P(ξ=3)=$\frac{{C}_{3}^{3}{C}_{3}^{0}}{{C}_{6}^{3}}$=$\frac{1}{20}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{20}$ | $\frac{9}{20}$ | $\frac{9}{20}$ | $\frac{1}{20}$ |
点评 本题考查回归方程的求法,考查离散型随机变量的分布列和数学期望的求法,考查推理论证能力、运算求解能力,考查等价转化思想,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{5}{4}+ln2,2})$ | B. | $[{2-ln2,\frac{5}{4}+ln2})$ | C. | $({\frac{5}{4}+ln2,2-ln2}]$ | D. | (2-ln2,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
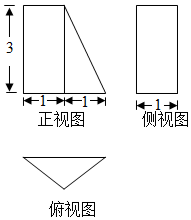 已知某几何体的三视图如图所示,该几何体的体积为( )
已知某几何体的三视图如图所示,该几何体的体积为( )| A. | $\frac{2}{3}$ | B. | 2 | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{3}{16}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x0∈R+,x02-x0<0”的否定是“?x∈R-,x2-x≥0” | |
| B. | 命题“若a≠b,则a2≠b2”的否命题是“若a≠b,则a2=b2” | |
| C. | x1>1且x2>1的充要条件是x1+x2>2. | |
| D. | p,q为两个命题,若p∨q为真且p∧q为假,则p,q两个命题中必有一个为真,一个为假. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com