
| A. | $[{\frac{5}{4}+ln2,2})$ | B. | $[{2-ln2,\frac{5}{4}+ln2})$ | C. | $({\frac{5}{4}+ln2,2-ln2}]$ | D. | (2-ln2,2] |
分析 由已知得到方程m=-lnx+3x-x2在[$\frac{1}{2}$,2]上有两解,构造函数h(x)=-lnx+3x-x2,求出h(x)的最值和端点值,即可得到m的范围.
解答 解:由已知得到方程f(x)=-g(x)在[$\frac{1}{2}$,2]上有两解,即m=-lnx+3x-x2在[$\frac{1}{2}$,2]上有解.
设h(x)=-lnx+3x-x2,则h′(x)=-$\frac{1}{x}$+3-2x=-$\frac{2{x}^{2}-3x+1}{x}$=-$\frac{(2x-1)(x-1)}{x}$,
令h′(x)=0得x=$\frac{1}{2}$或x=1.
∴当$\frac{1}{2}$<x<1时,f′(x)>0,当1<x<2时,f′(x)<0,
∴h(x)在($\frac{1}{2}$,1)上单调递增,在(1,2)上单调递减.
∴当x=1时,h(x)取得最大值h(1)=2,
∵h($\frac{1}{2}$)=ln2+$\frac{5}{4}$,h(2)=-ln2+2,且h(2)<h($\frac{1}{2}$),
$\frac{5}{4}$+ln2≤m<2.
从而m的取值范围为[$\frac{5}{4}$+ln2,2).
故选:A.
点评 本题考查了构造函数法求方程的解及参数范围;关键是将已知转化为方程x2+m=ln$\frac{1}{x}$+3x?m=-lnx+3x-x2在上有两解,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $-\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
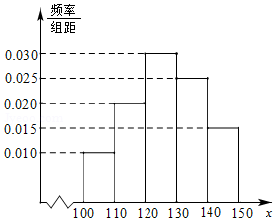 扶贫工作组帮助某村成立菠萝加工厂,加工菠萝罐头销售.在一个生产季内,销售1吨菠萝罐头可获利0.5万元,未销售的每吨亏损0.1万元.根据历年统计数据得到在生产季内菠萝罐头市场需求量x(100≤x≤150,单位:吨)的频率分布直方图如图.已知该厂在下一生产季计划生产130吨菠萝罐头.
扶贫工作组帮助某村成立菠萝加工厂,加工菠萝罐头销售.在一个生产季内,销售1吨菠萝罐头可获利0.5万元,未销售的每吨亏损0.1万元.根据历年统计数据得到在生产季内菠萝罐头市场需求量x(100≤x≤150,单位:吨)的频率分布直方图如图.已知该厂在下一生产季计划生产130吨菠萝罐头.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
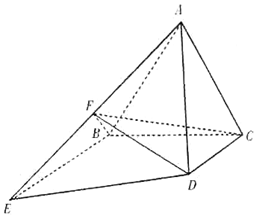 如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.
如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
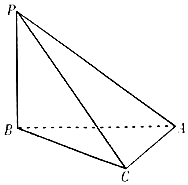 如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=$\sqrt{3}CA=\sqrt{3}$,则三棱锥P-ABC的外接球体积为$\frac{4π}{3}$.
如图,三棱锥P-ABC中,PB⊥BA,PC⊥CA,且PC=$\sqrt{3}CA=\sqrt{3}$,则三棱锥P-ABC的外接球体积为$\frac{4π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年宣传费x(万元) | 38 | 48 | 58 | 68 | 78 | 88 |
| 年销售量y(吨) | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
| $\sum_{i=1}^{6}$(lnxi•lnyi) | $\sum_{i=1}^{6}$(lnxi) | $\sum_{i=1}^{6}$(lnyi) | $\sum_{i=1}^{6}$(lnxi)2 |
| 75.3 | 24.6 | 18.3 | 101.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,6] | B. | [-3,5] | C. | [2,6] | D. | [3,5] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com