
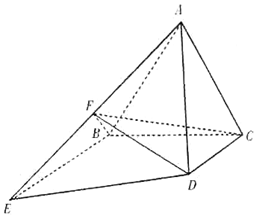
 如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.
如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AE的中点.分析 (1),取AB中点G,连接CG、FG,可得四边形CDFG为平行四边形,即DF∥CG,DF∥平面ABC.
(2)可得BE⊥面ABC,BE⊥CG. 即CG⊥面ABE,又DF∥CG,⇒DF⊥面ABE.
(3)取BC中点O,再连接AO,OD.易证AO⊥面BCDE,所以∠ADO为直线AD与平面BCDE所成的角,即$tan∠ADO=\frac{{\sqrt{15}}}{5}$,设OC=t,可求得t=1.
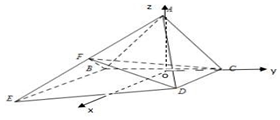
以O为原点,建立如图所示的空间直角坐标系O-xyz,则O(0,0,0),B(0,-1,0),C(0,1,0),D(2,1,0),利用向量法求解.
解答 解:(1)如图,取AB中点G,连接CG、FG,因为F为AE中点,所以FG∥BE且$FG=\frac{1}{2}CD$,BE=2CD,
所以FG∥CD且FG=CD,所以四边形CDFG为平行四边形,
所以DF∥CG.CG?平面ABC,DF?平面ABC,
∴DF∥平面ABC.
(2)又因为△ABC为正三角形,所以CG⊥AB,
又因为面ABC⊥面BCDE,面ABC∩面BCDE=BC.BE⊥BC,BE?面BCDE,
所以BE⊥面ABC,BE⊥CG.又因为BE∩AB=B,所以CG⊥面ABE,所以DF⊥面ABE.
(3)
取BC中点O,再连接AO,OD.
易证AO⊥面BCDE,所以∠ADO为直线AD与平面BCDE所成的角,
即$tan∠ADO=\frac{{\sqrt{15}}}{5}$,设OC=t,可求得t=1.
以O为原点,建立如图所示的空间直角坐标系O-xyz,
则O(0,0,0),B(0,-1,0),C(0,1,0),D(2,1,0),$E({4,-1,0}),A({0,0,\sqrt{3}}),F({2,-\frac{1}{2},\frac{{\sqrt{3}}}{2}})$,
所以$\overrightarrow{BF}=({2,\frac{1}{2},\frac{{\sqrt{3}}}{2}}),\overrightarrow{BC}=({0,2,0}),\overrightarrow{DC}=({-2,0,0}),\overrightarrow{DF}=({0,-\frac{3}{2},\frac{{\sqrt{3}}}{2}})$,
设平面BCF的法向量为$\overrightarrow n=({{n_1},{n_2},{n_3}})$,则$\left\{{\begin{array}{l}{2{n_2}=0}\\{2{n_1}+\frac{1}{2}{n_2}+\frac{{\sqrt{3}}}{2}{n_3}=0}\end{array}}\right.$,
令${n_1}=\sqrt{3}$,得n2=0,n3=-4,所以$\overrightarrow{n}=(\sqrt{3},0,-4)$,
设面DCF的法向量为$\overrightarrow{m}=({m}_{1},{m}_{2},{m}_{3})$,
则$\left\{{\begin{array}{l}{-2{m_1}=0}\\{-\frac{3}{2}{m_2}+\frac{{\sqrt{3}}}{2}{m_3}=0}\end{array}}\right.$,令m2=1,得${m_3}=\sqrt{3}$,m1=0,
所以$\overrightarrow{m}=(0,1,\sqrt{3})$,所以cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{-2\sqrt{51}}{19}$,
因为二面角B-CF-D为钝角,其余弦值为$\frac{{-2\sqrt{51}}}{19}$.
点评 本题考查了空间线面平行、线面垂直的判断,向量法求二面角,属于中档题.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{5}{4}+ln2,2})$ | B. | $[{2-ln2,\frac{5}{4}+ln2})$ | C. | $({\frac{5}{4}+ln2,2-ln2}]$ | D. | (2-ln2,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-4,-2] | B. | [-4,+∞) | C. | [-3,+∞) | D. | [-3,-2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±x | B. | y=±$\sqrt{2}$x | C. | y=±$\sqrt{3}$x | D. | y=±2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com