练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．已知直线l的参数方程为$\left\{\begin{array}{l}x=-1+\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t\end{array}\right.$（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为ρ=2cosθ．
    （Ⅰ）求直线l的普通方程与圆C的直角坐标方程；
    （Ⅱ）点P、Q分别在直线l和圆C上运动，求|PQ|的最小值．

    分析 （I）直线l的参数方程为$\left\{\begin{array}{l}x=-1+\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t\end{array}\right.$（t为参数），消去参数t可得：直线l的普通方程．圆C的极坐标方程为ρ=2cosθ，即ρ2=2ρcosθ，利用互化公式可得圆C的直角坐标方程．
    （Ⅱ） 由平面几何知识知：最小值为圆心C到l的距离减半径，利用点到直线的距离公式可得圆心C到l的距离d．

    解答 解：（I）直线l的参数方程为$\left\{\begin{array}{l}x=-1+\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t\end{array}\right.$（t为参数），消去参数t可得：直线l的普通方程为x-y+1=0．
    圆C的极坐标方程为ρ=2cosθ，即ρ2=2ρcosθ，利用互化公式可得圆C的直角坐标方程：（x-1）2+y2=1．
    （Ⅱ） 由平面几何知识知：最小值为圆心C到l的距离减半径，∵圆心到直线的距离$d=\frac{{|{1+1}|}}{{\sqrt{2}}}=\sqrt{2}$．
    ∴|PQ|的最小值为$\sqrt{2}-1$．

    点评 本题考查了参数方程化为普通方程、极坐标化为直角坐标方程、直线与圆的位置关系、点到直线的距离公式，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    17．已知平面向量$\overrightarrow a$、$\overrightarrow b$都是单位向量，若$\overrightarrow b⊥（2\overrightarrow a-\overrightarrow b）$，则$\overrightarrow a$与$\overrightarrow b$的夹角等于（　　）
    A．$\frac{π}{6}$B．$\frac{π}{4}$C．$\frac{π}{3}$D．$\frac{π}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知θ是第四象限角，且$sin（θ+\frac{π}{4}）=\frac{3}{5}$，则$tan（θ-\frac{π}{4}）$=（　　）
    A．$\frac{3}{4}$B．$-\frac{3}{4}$C．$\frac{4}{3}$D．$-\frac{4}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知关于x的方程sinx+cosx=m在[0，π]有两个不等的实根，则m的一个值是（　　）
    A．0B．$\frac{1}{2}$C．$\frac{\sqrt{2}}{2}$D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．某程序框图如图所示，该程序运行后输出的S的值是（　　）
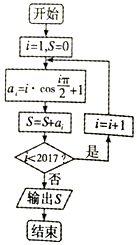
    A．1007B．3025C．2017D．3024

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知z=（m+4）+（m-2）i在复平面内对应的点在第三象限，则实数m的取值范围是（　　）
    A．（-4，2）B．（-2，4）C．（2，+∞）D．（-∞，-4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．（1）求不等式|x-5|-|2x+3|≥1的解集；
    （2）若正实数a，b满足$a+b=\frac{1}{2}$，求证：$\sqrt{a}+\sqrt{b}≤1$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．设x、y满足不等式组$\left\{\begin{array}{l}{x+y-2≥0}\\{x-y-10≤0}\\{y≤2}\end{array}\right.$，则z=x2+y2的最小值为（　　）
    A．$\sqrt{2}$B．$\frac{\sqrt{10}}{2}$C．2D．$\frac{5}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：万元）对年销售量y（单位：吨）的影响，对近六年的年宣传费xi和年销售量yi（i=1，2，3，4，5，6）的数据作了初步统计，得到如下数据：
     年份 2011 2012 2013 2014 2015 2016
     年宣传费x（万元） 3848  58 68 78 88
     年销售量y（吨） 16.8 18.8 20.7 22.4 24 25.5
    经电脑模拟发现年宣传费x（单位：万元）与年销售量y（单位：吨）之间近似满足关系式：y=a•xb（a，b＞G），即lny=b•lnx+lna，对上述数据作了初步处理，得到相关的值如下表：
     $\sum_{i=1}^{6}$（lnxi•lnyi） $\sum_{i=1}^{6}$（lnxi）  $\sum_{i=1}^{6}$（lnyi）  $\sum_{i=1}^{6}$（lnxi）2
     75.3 24.6 18.3 101.4
    （Ⅰ）根据所给数据，求y关于x的回归方程；
    （Ⅱ）规定当产品的年销售量y（单位：吨）与年宣传费x（单位：万元）的比值在区间（$\frac{e}{9}$，$\frac{e}{7}$）内时认为该年效益良好．现从这6年中任选3年，记其中选到效益良好的数量为ξ，求随机变量ξ的分布列和期望．（其中e为自然对数的底数，e≈2.7183）
    附：对于一组数据（u1，v1），（u2，v2），…，（un，vn），其回归直线v=β•u+a中的斜率和截距的最小二乘估计分别为：$\widehat{β}$=$\frac{\sum_{i=1}^{n}（{u}_{i}•{v}_{i}）-n（\overline{u}•\overline{v}）}{{\sum_{i=1}^{n}u}_{i}^{2}-n（\overline{u}）^{2}}$，$\stackrel{∧}{a}$=$\overline{v}$-$\stackrel{∧}{β}$•$\overline{u}$．

    查看答案和解析>>

    同步练习册答案