
【题目】已知曲线C1的极坐标方程为ρ=6cosθ,曲线C2的极坐标方程为θ= ![]() (p∈R),曲线C1 , C2相交于A,B两点. (Ⅰ)把曲线C1 , C2的极坐标方程转化为直角坐标方程;
(p∈R),曲线C1 , C2相交于A,B两点. (Ⅰ)把曲线C1 , C2的极坐标方程转化为直角坐标方程;
(Ⅱ)求弦AB的长度.
科目:高中数学 来源: 题型:
【题目】已知双曲线C1: ![]() =1,双曲线C2:
=1,双曲线C2: ![]() =1(a>0,b>0)的左、右焦点分别为F1 , F2 , M 是双曲线C2 一条渐近线上的点,且OM⊥MF2 , 若△OMF2的面积为 16,且双曲线C1 , C2的离心率相同,则双曲线C2的实轴长为( )
=1(a>0,b>0)的左、右焦点分别为F1 , F2 , M 是双曲线C2 一条渐近线上的点,且OM⊥MF2 , 若△OMF2的面积为 16,且双曲线C1 , C2的离心率相同,则双曲线C2的实轴长为( )
A.4
B.8
C.16
D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】极坐标系与直角坐标系xoy有相同的长度单位,以原点O为极点,以x轴正半轴为极轴.已知直线l的参数方程为  (t为参数),曲线C的极坐标方程为ρsin2θ=8cosθ. (I)求C的直角坐标方程;
(t为参数),曲线C的极坐标方程为ρsin2θ=8cosθ. (I)求C的直角坐标方程;
(Ⅱ)设直线l与曲线C交于A,B两点,求弦长|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,公比q>1,且满足a2+a3+a4=28,a3+2是a2与a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=log2an+5 , 且数列{bn}的前n项的和为Sn , 求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c.向量 ![]() =(a,
=(a, ![]() b)与
b)与 ![]() =(cosA,sinB)平行. (Ⅰ)求A;
=(cosA,sinB)平行. (Ⅰ)求A;
(Ⅱ)若a= ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正三棱柱ABC﹣A′B′C′如图所示,其中G是BC的中点,D,E分别在线段AG,A′C上运动,使得DE∥平面BCC′B′,CC′=2BC=4. 
(1)求二面角A′﹣B′C﹣C′的余弦值;
(2)求线段DE的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若命题p:从有2件正品和2件次品的产品中任选2件得到都是正品的概率为三分之一;命题q:在边长为4的正方形ABCD内任取一点M,则∠AMB>90°的概率为 ![]() ,则下列命题是真命题的是( )
,则下列命题是真命题的是( )
A.p∧q
B.(p)∧q
C.p∧(q)
D.q
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学开设甲、乙、丙三门选修课供学生任意选修(也可不选),假设学生是否选修哪门课彼此互不影响.已知某学生只选修甲一门课的概率为0.08,选修甲和乙两门课的概率为0.12,至少选修一门的概率是0.88.
(1)求该学生选修甲、乙、丙的概率分别是多少?
(2)用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如甲图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起到△D1AE位置,使平面D1AE⊥平面ABCE,得到乙图所示的四棱锥D1﹣ABCE.
(Ⅰ)求证:BE⊥平面D1AE;
(Ⅱ)求二面角A﹣D1E﹣C的余弦值.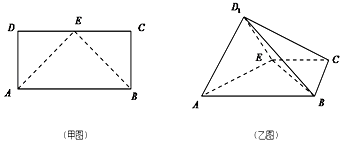
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com