
【题目】已知正三棱柱ABC﹣A′B′C′如图所示,其中G是BC的中点,D,E分别在线段AG,A′C上运动,使得DE∥平面BCC′B′,CC′=2BC=4. 
(1)求二面角A′﹣B′C﹣C′的余弦值;
(2)求线段DE的最小值.
【答案】
(1)解:如图,
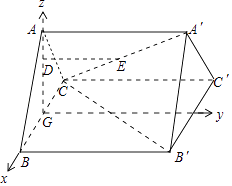
∵ABC﹣A′B′C′为正三棱柱,G是BC的中点,
∴AG⊥平面BCC′B′,以GB所在直线为x轴,以过G且垂直于BG的直线为y轴,以GA所在直线为z轴建立空间直角坐标系,
则G(0,0,0),A(0,0, ![]() ),C(﹣1,0,0),B′(1,4,0),A′(0,4,
),C(﹣1,0,0),B′(1,4,0),A′(0,4, ![]() ),
),
![]() =(1,4,
=(1,4, ![]() ),
), ![]() ,
,
平面B′CC′的一个法向量为 ![]() ,
,
设平面A′B′C的一个法向量为 ![]() ,
,
由 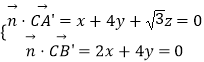 ,取y=1,得x=﹣2,z=
,取y=1,得x=﹣2,z= ![]() .
.
∴ ![]() ,
,
∴cos< ![]() >=
>= ![]() =
= 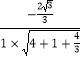 =
= ![]() .
.
∴二面角A′﹣B′C﹣C′的余弦值为 ![]() ;
;
(2)设D(0,0,t)(0≤t≤ ![]() ),E(x,y,z),
),E(x,y,z),
则 ![]() ,∴(x+1,y,z)=(λ,4λ,
,∴(x+1,y,z)=(λ,4λ, ![]() ),即x=λ﹣1,y=4λ,z=
),即x=λ﹣1,y=4λ,z= ![]() .
.
∴E(λ﹣1,4λ, ![]() ),
), ![]() =(λ﹣1,4λ,
=(λ﹣1,4λ, ![]() ),
),
由DE∥平面BCC′B′,得 ![]() ,得λ=
,得λ= ![]() .
.
∴ ![]() =
= ![]() ,
,
当t= ![]() 时,
时, ![]() 有最小值
有最小值 ![]() ,
,
∴线段DE的最小值为 ![]() .
.
【解析】(1)由题意画出图形,以GB所在直线为x轴,以过G且垂直于BG的直线为y轴,以GA所在直线为z轴建立空间直角坐标系,求出平面B′CC′与平面A′B′C的一个法向量,由两法向量所成角的余弦值求得二面角A′﹣B′C﹣C′的余弦值;(2)设D(0,0,t)(0≤t≤ ![]() ),E(x,y,z),由
),E(x,y,z),由 ![]() ,结合DE∥平面BCC′B′把λ用含有t的代数式表示,然后求出
,结合DE∥平面BCC′B′把λ用含有t的代数式表示,然后求出 ![]() 的最小值得答案.
的最小值得答案.


科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC. (Ⅰ)求证:AC⊥平面BDEF;
(Ⅱ)求证:FC∥平面EAD;
(Ⅲ)求二面角A﹣FC﹣B的余弦值.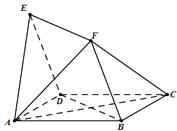
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,角A,B,C所对边分别是a、b、c,且cosA= ![]() .
.
(1)求sin2 ![]() +cos2A的值;
+cos2A的值;
(2)若a= ![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数 ![]() ,为了得到函数g(x)=sin2x的图象,则只需将f(x)的图象( )
,为了得到函数g(x)=sin2x的图象,则只需将f(x)的图象( )
A.向右平移 ![]() 个长度单位
个长度单位
B.向右平移 ![]() 个长度单位
个长度单位
C.向左平移 ![]() 个长度单位
个长度单位
D.向左平移 ![]() 个长度单位
个长度单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1的极坐标方程为ρ=6cosθ,曲线C2的极坐标方程为θ= ![]() (p∈R),曲线C1 , C2相交于A,B两点. (Ⅰ)把曲线C1 , C2的极坐标方程转化为直角坐标方程;
(p∈R),曲线C1 , C2相交于A,B两点. (Ⅰ)把曲线C1 , C2的极坐标方程转化为直角坐标方程;
(Ⅱ)求弦AB的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙两人每次射击命中目标的概率分别为 ![]() ,且各次射击相互独立,若按甲、乙、甲、乙…的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是( )
,且各次射击相互独立,若按甲、乙、甲、乙…的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin2x﹣2cos2x﹣1,x∈R.
sin2x﹣2cos2x﹣1,x∈R.
(Ⅰ)求函数f(x)的最小正周期和最小值;
(Ⅱ)在△ABC中,A,B,C的对边分别为a,b,c,已知c= ![]() ,f(C)=0,sinB=2sinA,求a,b的值.
,f(C)=0,sinB=2sinA,求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种产品的产量x(吨)与相应的生产成本y(万元)有如下几组样本数据:
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3.1 | 3.9 | 4.5 |
据相关性检验,这组样本数据具有线性相关关系,通过线性回归分析,求得到其回归直线的斜率为0.8,则当该产品的生产成本是6.7万元时,其相应的产量约是( )
A.8
B.8.5
C.9
D.9.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m﹣|x﹣2|,m∈R,且f(x+2)≥0的解集为[﹣3,3].
(Ⅰ)解不等式:f(x)+f(x+2)>0;
(Ⅱ)若a,b,c均为正实数,且满足a+b+c=m,求证: ![]() ≥3.
≥3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com