
(本小题满分14分)已知函数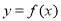 ,若在区间
,若在区间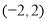 内有且仅有一个
内有且仅有一个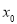 ,使得
,使得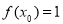 成立,则称函数
成立,则称函数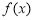 具有性质
具有性质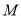 .
.
(Ⅰ)若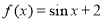 ,判断
,判断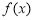 是否具有性质
是否具有性质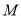 ,说明理由;
,说明理由;
(Ⅱ)若函数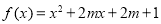 具有性质
具有性质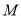 ,试求实数
,试求实数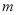 的取值范围.
的取值范围.
(Ⅰ) 具有性质
具有性质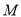 ; (Ⅱ)
; (Ⅱ) 或
或 或
或
【解析】
试题分析:(Ⅰ) 具有性质
具有性质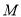 .若存在
.若存在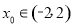 ,使得
,使得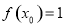 ,解方程求出方程的根,即可证得;(Ⅱ)依题意,若函数
,解方程求出方程的根,即可证得;(Ⅱ)依题意,若函数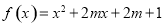 具有性质
具有性质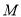 ,即方程
,即方程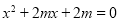 在
在 上有且只有一个实根.设
上有且只有一个实根.设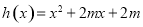 ,即
,即 在
在 上有且只有一个零点.讨论
上有且只有一个零点.讨论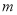 的取值范围,结合零点存在定理,即可得到
的取值范围,结合零点存在定理,即可得到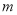 的范围.
的范围.
试题解析:(Ⅰ) 具有性质
具有性质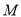 .
.
依题意,若存在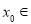
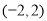 ,使
,使 ,则
,则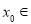
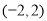 时有
时有 ,即
,即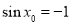 ,
, ,
,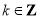 .由于
.由于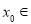
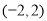 ,所以
,所以 .又因为区间
.又因为区间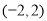 内有且仅有一个
内有且仅有一个 ,使
,使 成立,所以
成立,所以 具有性质
具有性质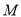 5分
5分
(Ⅱ)依题意,若函数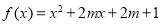 具有性质
具有性质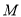 ,即方程
,即方程 在
在 上有且只有一个实根.
上有且只有一个实根.
设 ,即
,即 在
在 上有且只有一个零点.
上有且只有一个零点.
解法一:
(1)当 时,即
时,即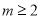 时,可得
时,可得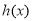 在
在 上为增函数,
上为增函数,
只需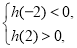 解得
解得 交集得
交集得 .
.
(2)当 时,即
时,即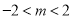 时,若使函数
时,若使函数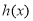 在
在 上有且只有一个零点,需考虑以下3种情况:
上有且只有一个零点,需考虑以下3种情况:
(ⅰ)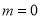 时,
时,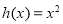 在
在 上有且只有一个零点,符合题意.
上有且只有一个零点,符合题意.
(ⅱ)当 即
即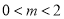 时,需
时,需 解得
解得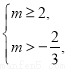 交集得
交集得 .
.
(ⅲ)当 时,即
时,即 时,需
时,需 解得
解得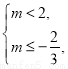 交集得
交集得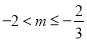 .
.
(3)当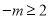 时,即
时,即 时,可得
时,可得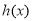 在
在 上为减函数
上为减函数
只需 解得
解得 交集得
交集得 .
.
综上所述,若函数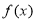 具有性质
具有性质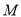 ,实数
,实数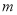 的取值范围是
的取值范围是 或
或 或
或 14分
14分
解法二:
依题意,
(1)由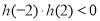 得,
得,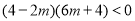 ,解得
,解得 或
或 .
.
同时需要考虑以下三种情况:
(2)由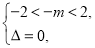 解得
解得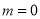 .
.
(3)由 解得
解得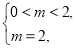 不等式组无解.
不等式组无解.
(4)由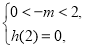 解得
解得 解得
解得 .
.
综上所述,若函数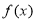 具有性质
具有性质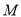 ,实数
,实数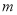 的取值范围是
的取值范围是 或
或
或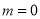 14分.
14分.
考点:1.零点存在定理;2.分类讨论的思想.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考文科数学试卷(解析版) 题型:选择题
下列命题中的假命题是( )
A、?x∈R,lgx=0
B、?x∈R,tanx=2
C、?x∈R,2x>0
D、?x∈R,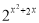 >1
>1
查看答案和解析>>
科目:高中数学 来源:2015届北京市朝阳区高三上学期期中统一考试理科数学试卷(解析版) 题型:填空题
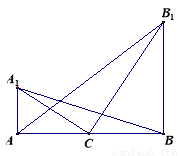
如图,在水平地面上有两座直立的相距60 m的铁塔 和
和 .已知从塔
.已知从塔 的底部看塔
的底部看塔 顶部的仰角是从塔
顶部的仰角是从塔 的底部看塔
的底部看塔 顶部的仰角的2倍,从两塔底部连线中点
顶部的仰角的2倍,从两塔底部连线中点 分别看两塔顶部的仰角互为余角.则从塔
分别看两塔顶部的仰角互为余角.则从塔 的底部看塔
的底部看塔 顶部的仰角的正切值为 ;塔
顶部的仰角的正切值为 ;塔 的高为 m.
的高为 m.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省烟台市高三统一质量检测考试理科数学试卷(解析版) 题型:解答题
一个空间几何体的三视图如下左图所示,则该几何体的表面积为( )
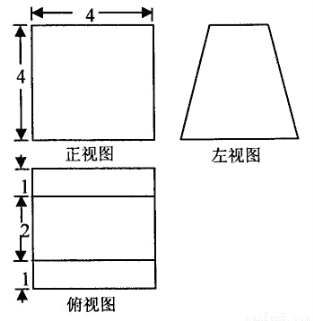
A.48 B.48+8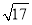 C.32+8
C.32+8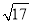 D.80
D.80
查看答案和解析>>
科目:高中数学 来源:2015届北京市朝阳区高三上学期期中统一考试文科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知数列 与
与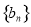 满足
满足 ,
, .
.
(Ⅰ)若
 ,求
,求 ,
, ;
;
(Ⅱ)若 ,求证:
,求证: ;
;
(Ⅲ)若 ,求数列
,求数列 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省烟台市高三5月适应性训练一理科数学试卷(解析版) 题型:解答题
己知函数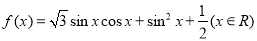
(1)当 时,求函数
时,求函数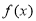 的最小值和最大值;
的最小值和最大值;
(2)设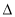 ABC的内角A,B,C的对应边分别为a,b,c,且c=
ABC的内角A,B,C的对应边分别为a,b,c,且c=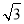 ,f(C)=2,若向量m=(1,a)与向量n=(2,b)共线,求a,b的值.
,f(C)=2,若向量m=(1,a)与向量n=(2,b)共线,求a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com