
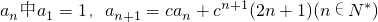 ,其中c≠0.
,其中c≠0. 通项公式;
通项公式;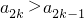 ,求c的取值范围.
,求c的取值范围.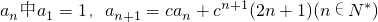 ,其中c≠0.
,其中c≠0.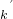 ,
, ,
, =
= .(10分)
.(10分) ,
, <
< =4k2+1,
=4k2+1,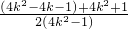 =
= ,…(11分)
,…(11分) =
=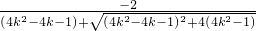 <0,
<0,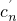 单调递增,故
单调递增,故 ≥
≥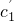 对一切k∈N*成立,
对一切k∈N*成立, 对一切k∈N*成立得c<
对一切k∈N*成立得c<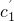 =-
=-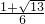 .…(13分)
.…(13分)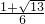 )∪[1,+∞).…(14分).
)∪[1,+∞).…(14分).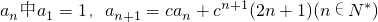 ,其中c≠0.求得a1=1,a2=ca1+c2•3=3c2+c,a3=ca2+c3•5=8c3+c2,由此猜测an=(n2-1)cn+cn-1,进而用数学归纳法证明.
,其中c≠0.求得a1=1,a2=ca1+c2•3=3c2+c,a3=ca2+c3•5=8c3+c2,由此猜测an=(n2-1)cn+cn-1,进而用数学归纳法证明.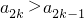 ,整理得(4k2-1)c2-(4k2-4k-1)c-1>0,设(4k2-1)c2-(4k2-4k-1)c-1=0的两个根分别表示ck和c
,整理得(4k2-1)c2-(4k2-4k-1)c-1>0,设(4k2-1)c2-(4k2-4k-1)c-1=0的两个根分别表示ck和c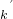 ,根据ck<
,根据ck<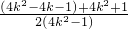 =
= ,得c≥1;再根据
,得c≥1;再根据 判断出单调递增知
判断出单调递增知 ≥
≥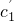 对一切k∈N*成立,求得c<-
对一切k∈N*成立,求得c<-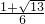 .最后综合答案可得.
.最后综合答案可得.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| a | n |
| a | 1 |
| a | n+1 |
| a | n |
| a | n |
| a | 2k |
| a | 2k-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 1 |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省黄冈市武穴中学高三(上)12月月考数学试卷(理科)(解析版) 题型:解答题
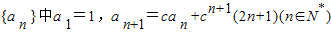 ,其中c≠0.
,其中c≠0.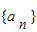 通项公式;
通项公式;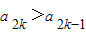 ,求c的取值范围.
,求c的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com