
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当函数![]() 有两个零点,求实数
有两个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)答案见解析;(2)![]() .
.
【解析】分析:(1)先求导,再对a分类讨论,求函数的单调区间. (2)对a分类讨论,作出函数的图像,分析出函数f(x)有两个零点所满足的条件,从而求出a的取值范围.
详解:(1)由题意得![]()
①当![]() 时,令
时,令![]() ,则
,则![]() ;
;
令![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
②当![]() 时,令
时,令![]() ,则
,则![]() 或
或![]() ,
,
(ⅰ)当![]() 时,令
时,令![]() ,则
,则![]() 或
或![]() ;
;
令![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
(ⅱ)当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递增;
上单调递增;
(ⅲ)当![]() 时,令
时,令![]() ,则
,则![]() 或
或![]() ;
;
令![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
(2)由(1)得当![]() 时,
时,![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() 在
在![]() 处取得极大值
处取得极大值![]() ,
,
∵![]() ,
,
∴此时不符合题意;
当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
∴此时不符合题意;
当![]() 时,
时,![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
∴![]() 的
的![]() 处取得极大值
处取得极大值![]() ,
,
∵![]() ,
,
∴此时不符合题意;
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∵![]() ,
,![]() ,
,
∴![]() 在
在![]() 上有一个零点,
上有一个零点,
(ⅰ)当![]() 时,令
时,令![]() ,当
,当![]() 时,
时,
∵![]() ,
,
∴![]() 在
在![]() 上有一个零点,
上有一个零点,
∴此时符合题意;
(ⅱ)当![]() 时,当
时,当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上没有零点,此时不符合题意;
上没有零点,此时不符合题意;
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】已知正方体![]() ,过对角线
,过对角线![]() 作平面
作平面![]() 交棱
交棱![]() 于点
于点![]() ,交棱
,交棱![]() 于点
于点![]() ,下列不正确的是( )
,下列不正确的是( )
A.平面![]() 分正方体所得两部分的体积相等;
分正方体所得两部分的体积相等;
B.四边形![]() 一定是平行四边形;
一定是平行四边形;
C.平面![]() 与平面
与平面![]() 不可能垂直;
不可能垂直;
D.四边形![]() 的面积有最大值.
的面积有最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品厂制作了3种与“福”字有关的精美卡片,分别是“富强福”、“和谐福”、“友善福”,每袋食品随机装入一张卡片,若只有集齐3种卡片才可获奖,则购买该食品4袋,获奖的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海域的东西方向上分别有A,B两个观测点(如图),它们相距![]() 海里.现有一艘轮船在D点发出求救信号,经探测得知D点位于A点北偏东45°,B点北偏西60°,这时,位于B点南偏西60°且与B点相距
海里.现有一艘轮船在D点发出求救信号,经探测得知D点位于A点北偏东45°,B点北偏西60°,这时,位于B点南偏西60°且与B点相距![]() 海里的C点有一救援船,其航行速度为30海里/小时.
海里的C点有一救援船,其航行速度为30海里/小时.

(1)求B点到D点的距离BD;
(2)若命令C处的救援船立即前往D点营救,求该救援船到达D点需要的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年“双十一”全网销售额达3143.25亿元,相当于全国人均消费225元,同比增长23.8%,监测参与“双十一”狂欢大促销的22家电商平台有天猫、京东、苏宁易购、网易考拉在内的综合性平台,有拼多多等社交电商平台,有敦煌网、速卖通等出口电商平台.某大学学生社团在本校1000名大一学生中采用男女分层抽样,分别随机调查了若干个男生和60个女生的网购消费情况,制作出男生的频率分布表、直方图(部分)和女生的茎叶图如下:
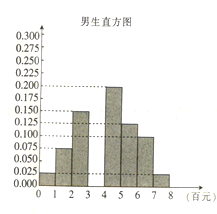
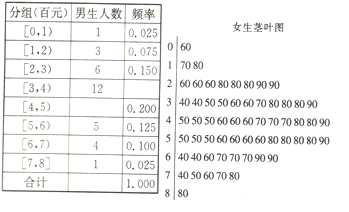
(1)请完成频率分布表的三个空格,并估计该校男生网购金额的中位数(单位:元,精确到个位).
(2)若网购为全国人均消费的三倍以上称为“剁手党”估计该校大一学生中的“剁手党”人数为多少?从抽样数据中网购不足200元的同学中随机抽取2人发放纪念品,则2人都是女生的概率为多少?
(3)用频率估计概率,从全市所有高校大一学生中随机调查5人,求其中“剁手党”人数的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个圆经过坐标原点和点(2,0),且圆心C在直线y=2x上.
(1)求圆C的方程;
(2)过点P(-2,2)作圆C的切线PA和PB,求直线PA和PB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 的普通方程;
的普通方程;
(2)设![]() 是曲线
是曲线![]() 上的一动点,求
上的一动点,求![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com