如图，在⊙O中，AB是弦，AC是⊙O的切线，A是切点，过 B作BD⊥AC于D，BD交⊙O于E点，若AE平分
∠BAD，则∠BAD=（ ）
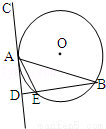
A.30° B.45° C.50° D.60°
科目：高中数学 来源：[同步]2014年新人教A版选修4-2 1.2二阶矩阵与平面向量的乘法（解析版） 题型：选择题
（2012•江门一模）定义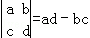
，其中a，b，c，d∈{﹣1，1，2，3，4}，且互不相等．则
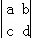的所有可能且互不相等的值之和等于（ ）
A.2012 B.﹣2012 C.0 D.以上都不对
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-1 3.2平面与圆柱面的截线练习卷（解析版） 题型：填空题
一只半径为R的球放在桌面上，桌面上一点A的正上方相距（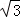
+1）R处有一点光源O，OA与球相切，则球在桌面上的投影——椭圆的离心率为 ．
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷（解析版） 题型：填空题
（2014•荆州二模）已知⊙O的半径R=2，P为直径AB延长线上一点，PB=3，割线PDC交⊙O于D，C两点，E为⊙O上一点，且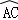
=
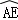，DE交AB于F，则OF= ．
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷（解析版） 题型：填空题
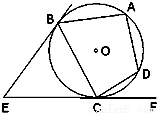
（2014•陕西模拟）如图，EB、EC是⊙O的两条切线，B、C是切点，A、D是⊙O上两点，如果∠E=46°，∠DCF=32°，则∠A的大小为 ．
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷（解析版） 题型：选择题
如图所示，CD切⊙O于B，CO的延长线交⊙O于A，若∠C=36°，则∠ABD的度数是（ ）
A.72° B.63° C.54° D.36°
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷（解析版） 题型：选择题
（2009•宣武区一模） 如图，AB是⊙O的直径，DE为⊙O的切线，切点为B，点C在⊙O上，若∠CBE=40°，则∠A的度数为（ ）
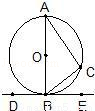
A.30° B.40° C.50° D.60°
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷（解析版） 题型：选择题
如图，△ABC内接于⊙O，∠A=40°，则∠OBC的度数为（ ）
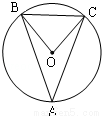
A.20° B.40° C.50° D.70°
查看答案和解析>>
科目：高中数学 来源：[同步]2014年北师大版选修1-2 3.2数学证明练习卷（解析版） 题型：选择题
（2014•潍坊三模）已知函数f（x）定义域为D，若?a，b，c∈D，f（a），f（b），f（c）都是某一三角形的三边，则称f（x）为定义在D上的“保三角形函数”，以下说法正确的个数有（ ）
①f（x）=1（x∈R）不是R上的“保三角形函数”
②若定义在R上的函数f（x）的值域为[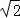
，2]，则f（x）一定是R上的“保三角形函数”
③f（x）=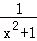
是其定义域上的“保三角形函数”
④当t＞1时，函数f（x）=ex+t一定是[0，1]上的“保三角形函数”
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
