练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图所示，CD切⊙O于B，CO的延长线交⊙O于A，若∠C=36°，则∠ABD的度数是（ ）

    A.72° B.63° C.54° D.36°

     

    B

    【解析】

    试题分析：连结OB，则∠OBC=90°．由已知条件求出∠A=27°．由此能求出∠ABD的度数．

    【解析】
    连结OB．∵CD为⊙O的切线，∴∠OBC=90°．

    ∵∠C=36°，∴∠BOC=54°．

    又∵∠BOC=2∠A，∴∠A=27°．

    ∴∠ABD=∠A+∠C=27°+36°=63°．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷（解析版） 题型：填空题

    将曲线 ，上所有点的横坐标扩大到原来的2倍，纵坐标缩小到原来的倍后，得到的曲线的焦点坐标为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-1 3.2平面与圆柱面的截线练习卷（解析版） 题型：填空题

    底面直径为12cm的圆柱被与底面成30°的平面所截，截口是一个椭圆，该椭圆的长轴长 ，短轴长 ，离心率为 ．

     

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷（解析版） 题型：填空题

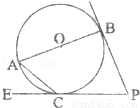
    （2014•河东区二模）如图，AB是⊙O的直径，PB，PC分别切⊙O于B，C，若∠ACE=38°，则∠P= ．

     

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷（解析版） 题型：选择题

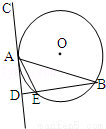
    如图，在⊙O中，AB是弦，AC是⊙O的切线，A是切点，过 B作BD⊥AC于D，BD交⊙O于E点，若AE平分

    ∠BAD，则∠BAD=（ ）

    A.30° B.45° C.50° D.60°

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷（解析版） 题型：选择题

    如图，△ABC内接于圆⊙O，CT切⊙O于C，∠ABC=100°，∠BCT=40°，则∠AOB=（ ）

    A.30° B.40° C.80° D.70°

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷（解析版） 题型：填空题

    （2010•嘉兴一模）如图所示．△ABC内接于⊙O，若∠OAB=28°，则∠C的大小是 ．

     

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷（解析版） 题型：选择题

    图中∠BOD的度数是（ ）

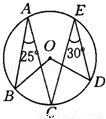
    A.55° B.110° C.125° D.150°

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修1-2 3.2数学证明练习卷（解析版） 题型：选择题

    （2014•揭阳三模）对于正实数α，Mα为满足下述条件的函数f（x）构成的集合：?x1，x2∈R且x2＞x1，有﹣α（x2﹣x1）＜f（x2）﹣f（x1）＜α（x2﹣x1）．下列结论中正确的是（ ）

    A.若f（x）∈Mα1，g（x）Mα2，则f（x）•g（x）∈Mα1•α2

    B.若f（x）∈Mα1，g（x）∈Mα2，且g（x）≠0，则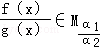

    C.若f（x）∈Mα1，g（x）∈Mα2，则f（x）+g（x）∈Mα1+α2

    D.若f（x）∈Mα1，g（x）∈Mα2，且α1＞α2，则f（x）﹣g（x）∈Mα1﹣α2

     

    查看答案和解析>>

    同步练习册答案