练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，△ABC内接于圆⊙O，CT切⊙O于C，∠ABC=100°，∠BCT=40°，则∠AOB=（ ）

    A.30° B.40° C.80° D.70°

     

    C

    【解析】

    试题分析：由圆周角定理知，欲求∠AOB，需求出∠ACB的度数；在△ABC中，已知∠ABC的度数，而根据弦切角定理，可得出∠CAB的度数；再，由三角形内角和定理，可求出∠ACB的度数，由此得解．

    【解析】
    ∵CT切⊙O于C

    ∴∠BAC=∠BCT=40°；

    在△ABC中，∠BAC=40°，∠ABC=100°，

    ∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣40°﹣100°=40°，

    ∴∠AOB=2∠ACB=2×40°=80°．

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷（解析版） 题型：填空题

    将曲线x+y2=1绕原点逆时针旋转45°后，得到的曲线C方程为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-1 3.1平行射影练习卷（解析版） 题型：填空题

    平行投影与中心投影之间的区别是 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷（解析版） 题型：填空题

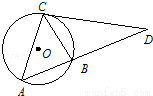
    （2014•渭南二模）如图，圆O是△ABC的外接圆，过点C的切线交AB的延长线于点D，CD=2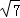，AB=BC=3．AC的长为 ．

     

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷（解析版） 题型：选择题

    如图所示，CD切⊙O于B，CO的延长线交⊙O于A，若∠C=36°，则∠ABD的度数是（ ）

    A.72° B.63° C.54° D.36°

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷（解析版） 题型：选择题

    （2014•石景山区一模）已知Rt△ABC中，∠C=90°，AB=5，BC=4，以BC为直径的圆交AB于D，则BD的长为（ ）

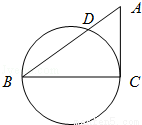
    A.4 B.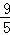 C. D.

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷（解析版） 题型：填空题

    （2012•密云县一模）如图所示，AB与CD是⊙O的直径，AB⊥CD，P是AB延长线上一点，连PC交⊙O于点E，连DE交AB于点F，若AB=2BP=4，则PF= ．

     

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷（解析版） 题型：选择题

    （2010•泰安二模）如图所示，已知⊙O是△ABC的外接圆，AD是⊙O的直径，连接CD，若AD=3，AC=2，则cosD的值为（ ）

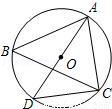
    A. B. C. D.

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修1-2 2.2结构图练习卷（解析版） 题型：填空题

    现有爬行、哺乳、飞行三类动物，其中蛇、地龟属于爬行动物；狼、狗属于 哺乳动物；鹰、长尾雀属于飞行动物，请你把下列结构图补充完整．

     

     

    查看答案和解析>>

    同步练习册答案