
一只半径为R的球放在桌面上,桌面上一点A的正上方相距(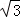 +1)R处有一点光源O,OA与球相切,则球在桌面上的投影——椭圆的离心率为 .
+1)R处有一点光源O,OA与球相切,则球在桌面上的投影——椭圆的离心率为 .

【解析】
试题分析:根据圆曲线的第一定义,作出过圆锥的轴与椭圆长轴AA′的截面,可得直角三角形AOA′,结合已知求出椭圆的a值,再根据椭圆的几何性质,求出c,即可求出椭圆的离心率.
【解析】
如图是过圆锥的轴与椭圆长轴AA′的截面,
ED两点为过点O引圆D的两条切线与圆D的切点,
∵OA=(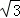 +1)R,
+1)R,
故在Rt△OBE中,
OE=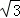 R,BE=R,
R,BE=R,
则tan∠EOB=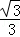 ,
,
即∠EOB=30°,
故∠EOB=60°,即∠AOA′=60°,
故AA′=2a=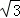 OA=(3+
OA=(3+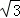 )R,即a=
)R,即a= ,
,

根据圆锥曲线的定义,
可得球与长轴AA′的切点是椭圆的焦点F,
根据椭圆的几何性质,AF是焦点到长轴顶点的距离AF=a﹣c=R,
∴c= =
= a,
a,
所求椭圆的离心率e=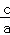 =
= ,
,
故答案为:


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.3线性变换的基本性质练习卷(解析版) 题型:选择题
圆x2+y2=1在矩阵A=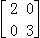 对应的变换下,得到的曲线的方程是( )
对应的变换下,得到的曲线的方程是( )
A.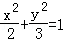 B.
B.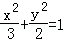 C.
C.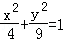 D.
D.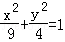
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:填空题
直线y=3x绕原点逆时针旋转90°,再向右平移1个单位,所得到的直线为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:选择题
对于函数f(x),如果存在锐角θ使得f(x)的图象绕坐标原点逆时针旋转角θ,所得曲线仍是一函数,则称函数f(x)具备角θ的旋转性,下列函数具有角 的旋转性的是( )
的旋转性的是( )
A. B.y=lnx C.
B.y=lnx C. D.y=x2
D.y=x2
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.3平面与圆锥面的截线练习卷(解析版) 题型:填空题
在空间中,取直线l为轴,直线l′与l相交于点O,其夹角为α(α为锐角),l′围绕l旋转得到以O为顶点,l′为母线的圆锥面,任取平面π,若它与轴l交角为β(π与l平行时,记β=0),则:当 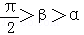 时,平面π与圆锥面的交线为 .
时,平面π与圆锥面的交线为 .

查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.2平面与圆柱面的截线练习卷(解析版) 题型:填空题
底面直径为12cm的圆柱被与底面成30°的平面所截,截口是一个椭圆,该椭圆的长轴长 ,短轴长 ,离心率为 .

查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.1平行射影练习卷(解析版) 题型:填空题
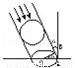
如图,一个广告气球被一束入射角为α的平行光线照射,其投影是一个长半轴为5 m的椭圆,则制作这个广告气球至少需要的面料是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:选择题
如图,在⊙O中,AB是弦,AC是⊙O的切线,A是切点,过 B作BD⊥AC于D,BD交⊙O于E点,若AE平分
∠BAD,则∠BAD=( )
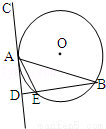
A.30° B.45° C.50° D.60°
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修1-2 3.3综合法与分析法练习卷(解析版) 题型:选择题
下列表述:①综合法是执因导果法;②综合法是顺推法;③分析法是执果索因法;
④分析法是间接证法;⑤反证法是逆推法.正确的语句有( )
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com