
【题目】已知焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() (
(![]() ,
,![]() )与椭圆C交于两点A、B,点D满足
)与椭圆C交于两点A、B,点D满足![]() ,经过点D及点
,经过点D及点![]() 的直线的斜率为
的直线的斜率为![]() ,求证:
,求证:![]() .
.
【答案】(I)![]() ;(II)详见解析.
;(II)详见解析.
【解析】
(Ⅰ)设椭圆C的标准方程为![]() (a>b>0),根据a2=b2+c2,椭圆C过点(0,1),离心率为
(a>b>0),根据a2=b2+c2,椭圆C过点(0,1),离心率为![]() ,即可求得椭圆C的标准方程;
,即可求得椭圆C的标准方程;
(Ⅱ)由题意知点D为线段AB的中点,设A(x1,y1),B(x2,y2),G(xD,yD),由题意知xD=﹣4kyD,![]() ,从而求出
,从而求出![]() ,进而得到
,进而得到![]() ,由此可知
,由此可知![]() .
.
(Ⅰ)设椭圆![]() 的标准方程为
的标准方程为![]() ,且
,且![]() .
.
由题意可知:![]() ,
,![]() .所以
.所以![]() .
.
所以,椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)方法一:![]()
![]() ,点D为线段AB的中点
,点D为线段AB的中点
设![]()
![]() ,
,
 ,∴
,∴![]()
由![]() ,得
,得![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,∴
,∴![]() .
.
方法2:![]()
![]() ,点D为线段AB中点,
,点D为线段AB中点,
设![]()
![]() ,
, ,∴
,∴![]() ,
,
由![]() ,得
,得![]() ,
,
∵![]() ,∴
,∴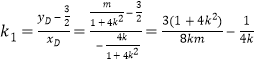 ,
,
![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]() .
.
方法3:由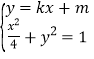 ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
设![]() ,
,![]()
![]()
![]() ,点D为线段AB的中点,
,点D为线段AB的中点,
设![]() ,
,![]() ,
,
∵![]() ,∴
,∴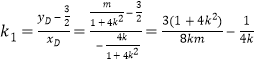 ,
,
![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】有如下3个命题;
①双曲线![]() 上任意一点
上任意一点![]() 到两条渐近线的距离乘积是定值;
到两条渐近线的距离乘积是定值;
②双曲线![]() 的离心率分别是
的离心率分别是![]() ,则
,则![]() 是定值;
是定值;
③过抛物线![]() 的顶点任作两条互相垂直的直线与抛物线的交点分别是
的顶点任作两条互相垂直的直线与抛物线的交点分别是![]() ,则直线
,则直线![]() 过定点;其中正确的命题有( )
过定点;其中正确的命题有( )
A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的程序框图的算法思路源于我国古代数学中的秦九韶算法,执行该程序框图,则输出的结果S表示的值为( ) 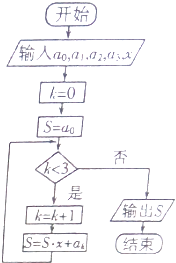
A.a0+a1+a2+a3
B.(a0+a1+a2+a3)x3
C.a0+a1x+a2x2+a3x3
D.a0x3+a1x2+a2x+a3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2ωx(ω>0),将y=f(x)的图象向右平移 ![]() 个单位长度后,若所得图象与原图象重合,则ω的最小值等于( )
个单位长度后,若所得图象与原图象重合,则ω的最小值等于( )
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC= ![]() AB=
AB= ![]() ,平面PBC⊥平面ABCD.
,平面PBC⊥平面ABCD. 
(1)求证:AC⊥PB;
(2)若PB=PC= ![]() ,问在侧棱PB上是否存在一点M,使得二面角M﹣AD﹣B的余弦值为
,问在侧棱PB上是否存在一点M,使得二面角M﹣AD﹣B的余弦值为 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的中位数是83,乙班学生成绩的平均数是86,则x+y的值为( ) 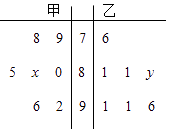
A.168
B.169
C.8
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:α∈R,sin(π﹣α)=cosα;命题q:“0<a<4”是“关于x的不等式ax2+ax+1>0的解集是实数集R”的充分必要条件,则下面结论正确的是( )
A.p是假命题
B.q是真命题
C.“p∧q”是假命题
D.“p∨q”是假命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com