
如图,在矩形 中,
中, ,
, 是
是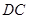 的中点,以
的中点,以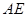 为折痕将
为折痕将 向上折起,使
向上折起,使 到
到 点位置,且
点位置,且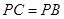 .
.
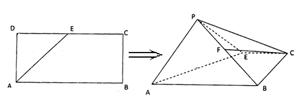
(Ⅰ)若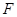 是
是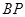 的中点,求证:
的中点,求证: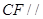 面
面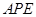 ;
;
(Ⅱ)求证:面 面
面 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
(Ⅰ)取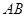 中点
中点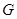 ,连接GF,GC,
,连接GF,GC,
由四边形AECG为平行四边形,
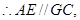 在
在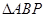 中,GF//AP,
中,GF//AP,
推出平面APE//平面FGC ;
又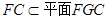 所以,CF//面APE.
所以,CF//面APE.
(Ⅱ)取AE中点O,连接PO,得到
取BC的中点H,连OH,PH,得到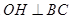
由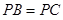 推出
推出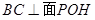 ,
, 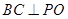 , 可得
, 可得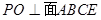
所以,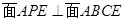 .
.
(Ⅲ)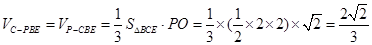 .
.
【解析】
试题分析:(Ⅰ)取 中点
中点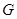 ,连接GF,GC,
,连接GF,GC,
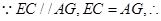 四边形AECG为平行四边形,
四边形AECG为平行四边形,
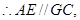
在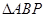 中,GF//AP,
中,GF//AP,
又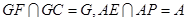 ,
,
所以平面APE//平面FGC
又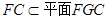 所以,CF//面APE.
4分
所以,CF//面APE.
4分
(Ⅱ)取AE中点O,连接PO,则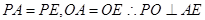
取BC的中点H,连OH,PH,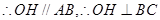
因为 所以
所以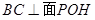 ,从而
,从而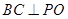 ,
,
又BC与AE相交,可得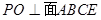
所以,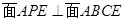 . 9分
. 9分
(Ⅲ)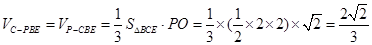 . 13分
. 13分
考点:本题主要考查立体几何中的平行关系、垂直关系,体积的计算。
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离及体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,利用向量则能简化证明过程。折叠问题,要注意折叠前后几何量的“变与不变”。本题(3)体积计算中运用了“等体积法”,化难为易。


科目:高中数学 来源:2014届广东省广州市高三9月三校联考文科数学试卷(解析版) 题型:解答题
如图,在多面体 中,四边形
中,四边形 是矩形,
是矩形, ∥
∥ ,
, ,平面
,平面 .
.

(1)若 点是
点是 中点,求证:
中点,求证: .
.
(2)求证: .
.
(3)若 求
求 .
.
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学必修3 3.3几何概型练习卷(一)(解析版) 题型:选择题
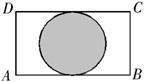
如图,在矩形 中,AB=4cm,BC=2cm,在图形上随机撒一粒黄豆,则黄豆落到阴影部分的概率是( )
中,AB=4cm,BC=2cm,在图形上随机撒一粒黄豆,则黄豆落到阴影部分的概率是( )
A.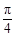 B.
B.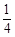
C.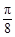 D.
D.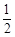
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com