
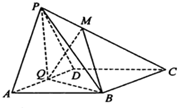
 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=AD=2.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD=AD=2.| n1 |
| n2 |
| 1 |
| 3 |
| PM |
| PC |
| AN |
| NC |
| 1 |
| 3 |
| 1 |
| 3 |
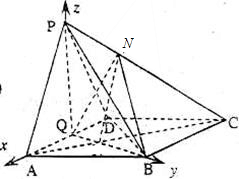 解:(1)由PA=PD=AD=2,Q为AD的中点,则PQ⊥AD…(2分)
解:(1)由PA=PD=AD=2,Q为AD的中点,则PQ⊥AD…(2分)| 3 |
| 3 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| QN |
| ||
| 2 |
| ||
| 2 |
| n1 |
| n1 |
| QN |
| n1 |
| QB |
|
| n1 |
| ||
| 2 |
| n2 |
| n1 |
| n2 |
2
| ||
| 7 |
2
| ||
| 7 |
| 1 |
| 3 |
| AQ |
| BC |
| AN |
| NC |
| 1 |
| 2 |
| PM |
| PC |
| AN |
| NC |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014-2015学年山东省潍坊市高一上学期10月月考数学试卷(解析版) 题型:填空题
已知函数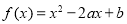 是定义在区间
是定义在区间 上的偶函数,求函数
上的偶函数,求函数 的值域为__________________
的值域为__________________
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省赣州市北校高二1月月考文科数学试卷(解析版) 题型:解答题
某校50名学生参加2013年全国数学联赛初赛,成绩全部介于90分到140分之间.将成绩结果按如下方式分成五组:第一组 ,第二组
,第二组 , ,第五组
, ,第五组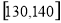 .按上述分组方法得到的频率分布直方图如图所示.
.按上述分组方法得到的频率分布直方图如图所示.
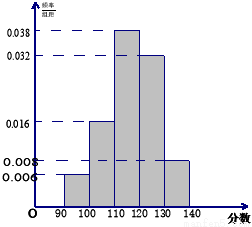
(1)若成绩大于或等于100分且小于120分认为是良好的,求该校参赛学生在这次数学联赛中成绩良好的人数;
(2)若从第一、五组中共随机取出两个成绩,求这两个成绩差的绝对值大于30分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在直三棱柱ABC-A1B1C1中,AB=BB1,D为AC的中点,AC1⊥平面A1BD.
如图,在直三棱柱ABC-A1B1C1中,AB=BB1,D为AC的中点,AC1⊥平面A1BD.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、(2,+∞) |
| B、(1,+∞) |
| C、(-∞,-2) |
| D、(-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ex |
| ex |
| 1 |
| g(x1) |
| 1 |
| g(x2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com