
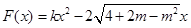 ,
,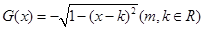
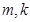 是常数,问当
是常数,问当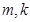 满足什么条件时,函数
满足什么条件时,函数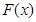 有最大值,并求出
有最大值,并求出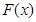 取最大值时
取最大值时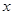 的值;
的值;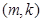 同时满足条件:(甲)
同时满足条件:(甲)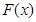 取最大值时
取最大值时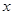 的值与
的值与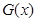 取最小值的
取最小值的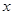 值相同,(乙)
值相同,(乙)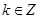 ?
?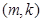 的集合记作A,设
的集合记作A,设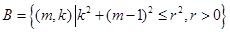 ,求使
,求使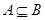 的
的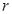 的取值范围.
的取值范围.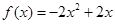 ,值域为
,值域为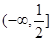 ;(2)证明见解析;(3)存在,且
;(2)证明见解析;(3)存在,且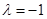 .
.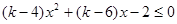 恒成立,那么这一定是二次不等式,恒成立的条件是
恒成立,那么这一定是二次不等式,恒成立的条件是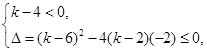 可解得
可解得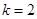 ,从而得到
,从而得到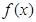 的解析式,其值域也易求得;(2)要证明数列
的解析式,其值域也易求得;(2)要证明数列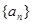 在该区间上是递增数列,即证
在该区间上是递增数列,即证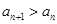 ,也即
,也即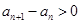 ,根据
,根据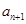 的定义,可把
的定义,可把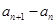 化为关于
化为关于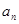 的二次函数,再利用
的二次函数,再利用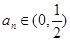 ,可得结论
,可得结论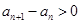 ;(3)这是一道存在性问题,解决问题的方法一般是假设存在符合题意的结论,本题中假设
;(3)这是一道存在性问题,解决问题的方法一般是假设存在符合题意的结论,本题中假设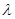 存在,使不等式成立,为了求出
存在,使不等式成立,为了求出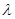 ,一般要把不等式左边的和求出来,这就要求我们要研究清楚第一项是什么?这个和是什么数列的和?由
,一般要把不等式左边的和求出来,这就要求我们要研究清楚第一项是什么?这个和是什么数列的和?由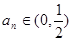 ,从而
,从而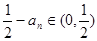 ,
,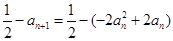
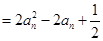
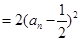 ,不妨设
,不妨设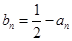 ,则
,则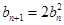 (
(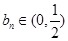 ),对这个递推公式我们可以两边取对数把问题转化为
),对这个递推公式我们可以两边取对数把问题转化为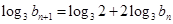 ,这是数列
,这是数列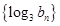 的递推公式,可以变为一个等比数列,方法是上式可变为
的递推公式,可以变为一个等比数列,方法是上式可变为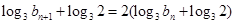 ,即数列
,即数列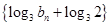 是公比为2的等比数列,其通项公式易求,反过来,可求得
是公比为2的等比数列,其通项公式易求,反过来,可求得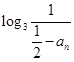 ,从而求出不等式左边的和,化简不等式.
,从而求出不等式左边的和,化简不等式.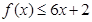 恒成立等价于
恒成立等价于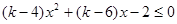 恒成立,
恒成立, 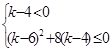 ,化简得
,化简得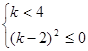 ,从而得
,从而得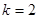 ,所以
,所以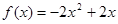 ,
,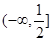 . 4分
. 4分
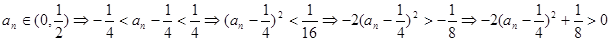 , 8分
, 8分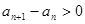 ,即
,即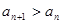 ,所以数列
,所以数列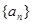 在区间
在区间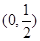 上是递增数列.
上是递增数列.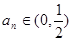 ,从而
,从而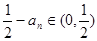 ;
;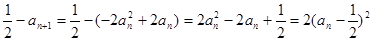 ,即
,即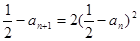 ;
;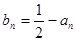 ,则有
,则有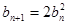 且
且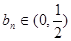 ;
;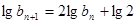 ,可得
,可得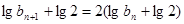 ,所以数列
,所以数列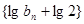 是
是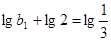 为首项,公比为
为首项,公比为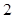 的等比数列,
的等比数列,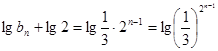 ,即
,即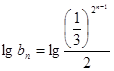 ,
,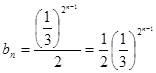 ,
,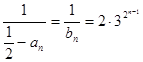 ,所以
,所以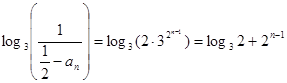 ,
,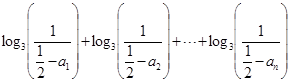
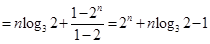 .
.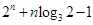
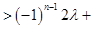
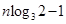 ,所以,
,所以,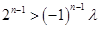 恒成立.
恒成立.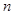 为奇数时,即
为奇数时,即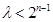 恒成立,当且仅当
恒成立,当且仅当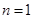 时,
时,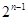 有最小值
有最小值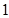 为.
为.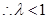
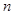 为偶数时,即
为偶数时,即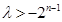 恒成立,当且仅当
恒成立,当且仅当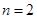 时,有最大值
时,有最大值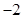 为.
为.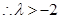
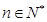 ,有
,有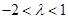 .又
.又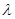 非零整数,
非零整数,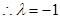
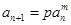 ,
,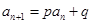 的数列通项公式,等比数列的前
的数列通项公式,等比数列的前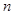 项和.
项和.

科目:高中数学 来源:不详 题型:填空题
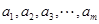 (
(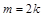 ,
,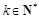 )满足条件
)满足条件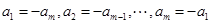 即
即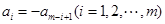 ,我们称其为“反对称数列”。
,我们称其为“反对称数列”。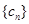 是项数为30的“反对称数列”,其中
是项数为30的“反对称数列”,其中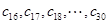 构成首项为-1,公比为2的等比数列.设
构成首项为-1,公比为2的等比数列.设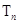 是数列
是数列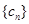 的前n项和,则
的前n项和,则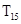 =
= 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
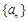 中,
中,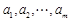 是首项为10,公差为
是首项为10,公差为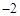 的等差数列;
的等差数列;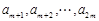 是首项为
是首项为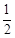 ,公比为
,公比为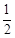 的等比数列(其中
的等比数列(其中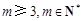 ),并且对于任意的
),并且对于任意的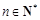 ,都有
,都有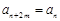 成立.若
成立.若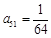 ,则m的取值集合为____________.记数列
,则m的取值集合为____________.记数列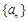 的前
的前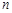 项和为
项和为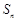 ,则使得
,则使得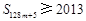
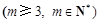 的
的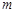 的取值集合为____________.
的取值集合为____________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com