
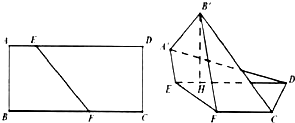
 已知矩形ABCD中,AB=2,AD=5.E,F分别在AD,BC上.且AE=1,BF=3,沿EF将四边形AEFB折成四边形A′EFB′,使点B′在平面CDEF 上的射影H在直线DE上.
已知矩形ABCD中,AB=2,AD=5.E,F分别在AD,BC上.且AE=1,BF=3,沿EF将四边形AEFB折成四边形A′EFB′,使点B′在平面CDEF 上的射影H在直线DE上.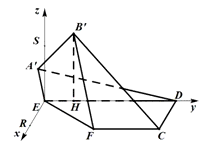 如图,过E作ER∥DC,过E作ES⊥平面EFCD,
如图,过E作ER∥DC,过E作ES⊥平面EFCD,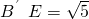 ,B′F=3.
,B′F=3.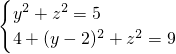 解得
解得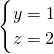 .
.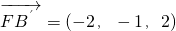 .
. =
=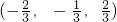 .
.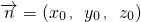 ,又有
,又有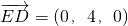 .
.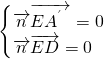 得
得 ,令x=1,则z=1,y═0,得到
,令x=1,则z=1,y═0,得到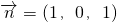 .
.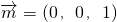 .
. =
= .
.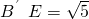 ,B′F=3,可得到点B′的坐标,分别求出平面A′DE的法向量、平面CDEF的法向量,利用法向量的夹角即可得到二面角.
,B′F=3,可得到点B′的坐标,分别求出平面A′DE的法向量、平面CDEF的法向量,利用法向量的夹角即可得到二面角.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
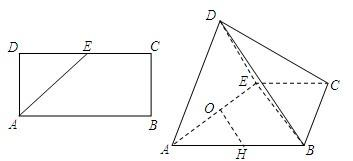 已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使DB=2
已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使DB=2| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•临沂二模)如图,已知矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将三角形AOD折起,使DB=
(2013•临沂二模)如图,已知矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将三角形AOD折起,使DB=| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com