
若在区域 内任取一点P,则点P落在单位圆
内任取一点P,则点P落在单位圆 内的概率为 .
内的概率为 .
解析试题分析:根据题意,区域D表示以原点、A(4,0)、B(0,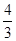 )为顶点的直角三角形,不难算出它的面积.而满足题意的点P落在落在单位圆x2+y2=1内,即落在图中圆心角为直角的扇形内,由此可得用扇形面积除以Rt△AOB面积,即得所求的概率.如图
)为顶点的直角三角形,不难算出它的面积.而满足题意的点P落在落在单位圆x2+y2=1内,即落在图中圆心角为直角的扇形内,由此可得用扇形面积除以Rt△AOB面积,即得所求的概率.如图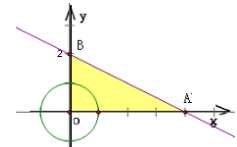
区域 表示的为以原点、A(4,0)、B(0,
表示的为以原点、A(4,0)、B(0,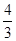 )为顶点的直角三角形,∵Rt△AOB与单位圆x2+y2=1的公共部分为圆心角为直角的扇形,其面积为S=
)为顶点的直角三角形,∵Rt△AOB与单位圆x2+y2=1的公共部分为圆心角为直角的扇形,其面积为S=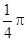 ,∴在Rt△AOB内任意取点P,能使P落在单位圆x2+y2=1内的概率为:
,∴在Rt△AOB内任意取点P,能使P落在单位圆x2+y2=1内的概率为: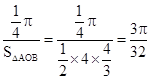 ,故填写
,故填写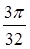
考点:本试题主要考查了以二元一次不等式组表示的平面区域为例,求几何概型的概率,着重考查了简单线性规划和几何概型的概率求法等知识,属于基础题.
点评:解决该试题的关键是对于题目中几何概型中事件表示的区域面积和整个事件的区域面积的求解。


科目:高中数学 来源: 题型:填空题
甲、乙两个袋中均有红、白两种颜色的小球,这些小球除颜色外完全相同,其中甲袋装有4个红球、2个白球, 乙袋装有1个红球、5个白球.现分别从甲、乙两袋中各随机取出一个球,则取出的两球都是红球的概率为 .(答案用分数表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com