
分析 (1)求出原函数的导函数,得到f′(1)=-1,即a=-1,再由(1,0)在直线g(x)=ax+b上求得b值;
(2)求出f′(x),g′(x),代入F(x)=x[f′(x)+g′(x)],然后求F(x)的导函数,由导函数的符号判断函数的单调性,求出极值点,代入函数F(x)求得极值.
解答 解:(1)由f(x)=lnx(lnx-1),得f′(x)=$\frac{1}{x}(lnx-1)+\frac{1}{x}lnx=\frac{2}{x}lnx-\frac{1}{x}$.
∴f′(1)=-1,即a=-1.
又(1,0)在直线g(x)=ax+b上,∴a+b=0,即b=-a=1;
(2)f′(x)=$\frac{2}{x}lnx-\frac{1}{x}$,g′(x)=-1,
∴F(x)=x[f′(x)+g′(x)]=x[$\frac{2}{x}lnx-\frac{1}{x}-1$]=2lnx-x-1.
F′(x)=$\frac{2}{x}-1=\frac{2-x}{x}$,
当x∈(0,2)时,F′(x)>0;当x∈(2,+∞)时,F′(x)<0.
∴当x=2时,函数F(x)取得极大值为F(2)=2ln2-3,无极小值.
点评 本题考查利用导数研究过曲线上某点处的切线方程,考查了利用导数求函数的极值,是中档题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | R | B. | (2,3) | C. | (-3,-2) | D. | (-3,-2)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
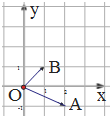 如图,在复平面内,复数z1,z2对应的向量分别是$\overrightarrow{OA}$,$\overrightarrow{OB}$,设复数$z=\frac{z_1}{z_2}$,则z的共轭复数为( )
如图,在复平面内,复数z1,z2对应的向量分别是$\overrightarrow{OA}$,$\overrightarrow{OB}$,设复数$z=\frac{z_1}{z_2}$,则z的共轭复数为( )| A. | $\frac{1}{2}-\frac{3}{2}i$ | B. | $\frac{1}{2}+\frac{3}{2}i$ | C. | 1-3i | D. | 1+3i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|a≥2} | B. | {a|a≤2} | C. | {a|-1≤a≤2} | D. | {a|-1≤a<2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com