
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
分析 由抛物线的方程找出p,写出抛物线的准线方程,因为准线方程与圆相切,所以圆心到直线的距离等于圆的半径,利用点到直线的距离公式列出关于m的方程,求出方程的解即可得到m的值.
解答 解:由抛物线的方程得到p=$\frac{1}{2m}$,所以抛物线的准线为y=-$\frac{1}{4m}$,
圆的圆心坐标为(0,0),圆的半径r=$\frac{1}{2}$,
圆心到直线的距离d=|-$\frac{1}{4m}$|=$\frac{1}{2}$,
∵m>0,∴解得m=$\frac{1}{2}$.
故选C.
点评 此题考查学生会求抛物线的准线方程,掌握直线与圆相切时所满足的条件,灵活运用点到直线的距离公式化简求值,是一道综合题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(2,+∞) | B. | $[-2\sqrt{3},-2)∪(2,2\sqrt{3}]$ | C. | $[2,2\sqrt{3})$ | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
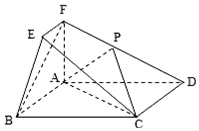 在如图所示的几何体中,四边形ABCD为矩形,平面ABCD⊥平面ABEF,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=1,点P在棱DF上.
在如图所示的几何体中,四边形ABCD为矩形,平面ABCD⊥平面ABEF,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=1,点P在棱DF上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若l∥α,l∥β,α∩β=m,则l∥m | B. | 若α⊥β,l⊥α,m⊥β则l⊥m | ||
| C. | 若α⊥β,α⊥γ,β∩γ=l,则l⊥α | D. | 若α∥β,l∥α,则l∥β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com