
| X | 1 | 2 | 3 | 4 |
| y | 1 | 3 | 5 | 6 |
分析 (1)把所给的四对数据写成对应的点的坐标,在坐标系中描出来,得到散点图.根据所给的这组数据求出利用最小二乘法所需要的几个数据,代入求系数b的公式,求得结果,再把样本中心点代入,求出a的值,得到线性回归方程.
(2)根据上一问所求的线性回归方程,把x=10代入线性回归方程,即可估计生产10吨A产品的生产能耗.
解答 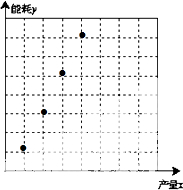 解:(1)散点图如图所示;
解:(1)散点图如图所示;
$\overline{x}$=2.5,$\overline{y}$=3.75,
∴b=$\frac{1+6+15+24-4×2.5×3.75}{1+4+9+16-4×6.25}$=1.7,
a=3.75-1.7×2.5=-0.5,
∴y=1.7x-0.5;
(2)x=10时,y=16.5,
∴预测生产A产品10(吨)时相应的生产能耗为16.5(吨).
点评 本题考查线性回归方程,两个变量之间的关系,除了函数关系,还存在相关关系,通过建立回归直线方程,就可以根据其部分观测值,获得对这两个变量之间整体关系的了解.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | $\sqrt{2}$ | C. | $\sqrt{13}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com