【答案】
分析:(1)利用二项式定理、二项式系数的性质化简S
n 为3
n+2
n,设n=2k,k∈z
+,则S
n-2
n-4n-1=3
n -4n-1=9
k-8k-1,用数学归纳法证明它能被64整除.
(2)分别令n=1、2、3 求出b
1 =1,b
2 =2,b
3=3,若存在等差数列{b
n},则 b
n =n,由C
n-11+C
n-12+C
n-13++C
n-1n-1 =
2
n-1 成立,可得C
n1+2C
n2+…+nC
nn=n(a
n-1)=n2
n-1 对一切n∈N
*都成立,故却是存在等差数列{b
n},满足条件.
(3)要证的不等式即:(1+

)(1+

)(1+

)…(1+

)≤3-

,用数学归纳法和放缩法证明此不等式成立.
解答:(1)证明:由已知得,S
n =a
1C
n+a
2C
n1+a
3C
n2+…+a
n+1C
nn=(1+1)C
n+(2+1)C
n1+(2
2+1)C
n2+…+(2
n)C
nn
=(C
n+2C
n1+2
2C
n2+…+2
nC
nn)+(C
n+C
n1+C
n2+…+C
nn)=(1+2)
n+2
n=3
n+2
n.
当n为偶数时,设n=2k,k∈z
+,则S
n-2
n-4n-1=3
n -4n-1=9
k-8k-1.
当k=1时,9
k-8k-1=0,显然能被64整除.
假设 9
m-8m-1 能被64整除m为正整数,则n=m+1时,9
k-8k-1=99
m-8m-8-1=9(9
m-8m-1 )+64m,
由假设知,9(9
m-8m-1 )能被64整除,再由64m 也能被64整除,
可得k=m+1时,9
m-8m-1仍能被64整除.
综上可得当n为偶数时,S
n-2
n-4n-1 能被64整除.
(2)∵b
1C
n1+b
2C
n2+…+b
nC
nn=n(a
n-1)对一切n∈N
*都成立,a
n=2
n-1+1,
故当n=1时,有 b
1 =a
1 -1=1,
当n=2时,有 2 b
1 +b
2 =2(a
2 -1)=4,∴b
2 =2.
当n=3时,有 3b
1 +3b
2+b
3=3(a
3-1),即 3+6+b
3=3×4,∴b
3=3.
若存在等差数列{b
n},使得b
1C
n1+b
2C
n2+…+b
nC
nn=n(a
n-1)对一切n∈N
*都成立,则应有b
n =n.
由二项式定理可得 C
n-11+C
n-12+C
n-13++C
n-1n-1 =2
n-1 成立,
故有n(C
n-1+C
n-11+C
n-12+C
n-13++C
n-1n-1)=n•2
n-1,即C
n1+2C
n2+…+nC
nn=n(a
n-1)=n2
n-1 对一切n∈N
*都成立,
故存在等差数列{b
n},使得b
1C
n1+b
2C
n2+…+b
nC
nn=n(a
n-1)对一切n∈N
*都成立,此时,b
n =n.
(3)T
n=1!C
n1+2!C
n2+3!C
n3+…+n!C
nn(n=1,2,3,…),
由题意可得

=

=

,∴3-

=3-

.
要证的不等式即:(1+

)(1+

)(1+

)…(1+

)≤3-

.
当n=2时,不等式的左边等于 (1+

)(1+

)=

,右边等于3-

=

,不等式成立.
假设n=k时,不等式成立,即:(1+

)(1+

)(1+

)…(1+

)≤3-

,
则n=k+1时,不等式的左边等于:(1+

)(1+

)(1+

)…(1+

)(1+

)≤(3-

)(1+
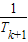
)
≤(3-

)(1+

)=3+

<3-

=3-

=右边,
故n=k+1时,(1+

)(1+

)(1+

)…(1+

)≤3-

也成立.
综上可得:(1+
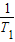
)(1+

)(1+

)…(1+

)≤3-

成立.
点评:本题主要考查用裂项法对数列进行求和,用数学归纳法证明等式和不等式,注意式子的结构特征,以及从n=k到n=k+1项的变化,属于难题.

 )(1+
)(1+ )(1+
)(1+ )…(1+
)…(1+ )≤3-
)≤3- .
. )(1+
)(1+ )(1+
)(1+ )…(1+
)…(1+ )≤3-
)≤3- ,用数学归纳法和放缩法证明此不等式成立.
,用数学归纳法和放缩法证明此不等式成立. =
= =
= ,∴3-
,∴3- =3-
=3- .
. )(1+
)(1+ )(1+
)(1+ )…(1+
)…(1+ )≤3-
)≤3- .
. )(1+
)(1+ )=
)= ,右边等于3-
,右边等于3- =
= ,不等式成立.
,不等式成立. )(1+
)(1+ )(1+
)(1+ )…(1+
)…(1+ )≤3-
)≤3- ,
, )(1+
)(1+ )(1+
)(1+ )…(1+
)…(1+ )(1+
)(1+ )≤(3-
)≤(3- )(1+
)(1+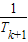 )
) )(1+
)(1+ )=3+
)=3+ <3-
<3- =3-
=3- =右边,
=右边, )(1+
)(1+ )(1+
)(1+ )…(1+
)…(1+ )≤3-
)≤3- 也成立.
也成立.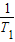 )(1+
)(1+ )(1+
)(1+ )…(1+
)…(1+ )≤3-
)≤3- 成立.
成立.
