
设f(x)=lnx,g(x)=f(x)+f ′(x).
(1)求g(x)的单调区间和最小值;
(2)讨论g(x)与g(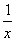 )的大小关系;
)的大小关系;
(3)求a的取值范围,使得g(a)-g(x)<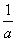 对任意x>0成立.
对任意x>0成立.
[解析] (1)g′(x)=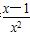 ,由g′(x)>0,得g(x)的单调增区间为(1,+∞);由g′(x)<0,得g(x)的单调减区间为(0,1).因此x=1是g(x)的唯一极值点,且为极小值点,从而是最小值点.所以g(x)min=g(1)=1.
,由g′(x)>0,得g(x)的单调增区间为(1,+∞);由g′(x)<0,得g(x)的单调减区间为(0,1).因此x=1是g(x)的唯一极值点,且为极小值点,从而是最小值点.所以g(x)min=g(1)=1.
(2)设h(x)=g(x)-g(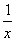 ),则h′(x)=-
),则h′(x)=-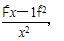 ,
,
h′(x)≤0,∴h(x)在(0,+∞)上为减函数.
当x=1时,h(1)=0,即g(x)=g(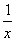 );
);
当0<x<1时,h(x)>h(1)=0,即g(x)>g(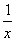 );
);
当x>1时,h(x)<h(1)=0,即g(x)<g(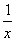 ).
).
(3)由(1)知g(x)的最小值为1,所以g(a)-g(x)<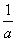 ,对任意x>0成立⇔由g(a)-1<
,对任意x>0成立⇔由g(a)-1<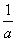 ,得0<a<e.
,得0<a<e.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
设函数f(x)=ax-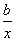 ,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
(1)求f(x)的解析式;
(2)证明:曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=ex(ax+b)-x2-4x,曲线y=f(x)在点(0,f(0))处的切线方程为y=4x+4.
(1)求a,b的值;
(2)讨论f(x)的单调性,并求f(x)的极大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,某农场要修建3个养鱼塘,每个面积为10 000m2,鱼塘前面要留4m的运料通道,其余各边为2m宽的堤埂,则占地面积最少时,每个鱼塘的长、宽分别为( )
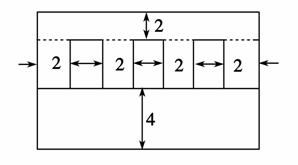
A.长102m,宽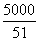 m B.长150m,宽66m
m B.长150m,宽66m
C.长、宽均为100米 D.长150m,宽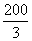 m
m
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)=-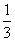 x3+
x3+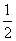 x2+2ax.
x2+2ax.
(1)若f(x)在(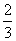 ,+∞)上存在单调递增区间,求a的取值范围.
,+∞)上存在单调递增区间,求a的取值范围.
(2)当0<a<2时,f(x)在[1,4]上的最小值为-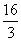 ,求f(x)在该区间上的最大值.
,求f(x)在该区间上的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com