
用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?最大容积是多少?
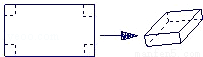
当高为10,最大容积为19600.
【解析】
试题分析:首先分析题目求长为90cm,宽为48cm的长方形铁皮做一个无盖的容器当容器的高为多少时,容器的容积最大.故可设容器的高为x,体积为V,求出v关于x的方程,然后求出导函数,分析单调性即可求得最值.
【解析】
根据题意可设容器的高为x,容器的体积为V,
则有V=(90﹣2x)(48﹣2x)x=4x3﹣276x2+4320x,(0<x<24)
求导可得到:V′=12x2﹣552x+4320
由V′=12x2﹣552x+4320=0得x1=10,x2=36.
所以当x<10时,V′>0,
当10<x<36时,V′<0,
当x>36时,V′>0,
所以,当x=10,V有极大值V(10)=19600,又V(0)=0,V(24)=0,
所以当x=10,V有最大值V(10)=19600
故答案为当高为10,最大容积为19600.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:填空题
(2013•珠海一模)(几何证明选讲选做题)
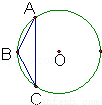
如图所示,等腰三角形ABC的底边AC长0为6,其外接圆的半径长为5,则三角形ABC的面积是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-2 3.2复数的四则运算练习卷(解析版) 题型:选择题
在复平面内,复数z=sin2+icos2对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-2 2.2直接证明与间接证明练习卷(解析版) 题型:填空题
设x,y,z是空间的不同直线或不同平面,且直线不在平面内,下列条件中能保证“若x⊥z,且y⊥z,则x∥y”为真命题的是 (填所有正确条件的代号)
①x为直线,y,z为平面;
②x,y,z为平面;
③x,y为直线,z为平面;
④x,y为平面,z为直线;
⑤x,y,z为直线.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-2 2.2直接证明与间接证明练习卷(解析版) 题型:选择题
设x,y,z∈(0,+∞),a=x+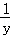 ,b=y+
,b=y+ ,c=z+
,c=z+ ,则a,b,c三数( )
,则a,b,c三数( )
A.至少有一个不大于2 B.都小于2
C.至少有一个不小于2 D.都大于2
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 3.4导数在实际生活中的应用练习卷(解析版) 题型:填空题
设底为等边三角形的直棱柱的体积为V,那么其表面积最小时,底面边长为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 3.4导数在实际生活中的应用练习卷(解析版) 题型:填空题
某商品一件的成本为30元,在某段时间内,若以每件x元出售,可卖出(200﹣x)件,当每件商品的定价为 元时,利润最大.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 2.5圆锥曲线与方程练习卷(解析版) 题型:解答题
将曲线log2x+log2y=2沿x、y轴﹣分别向右平移两个单位,向上平移一个单位,此时直线x+y+a=0与此曲线仅有一个公共点,求实数a的值.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 2.1圆锥曲线练习卷(解析版) 题型:填空题
若直线x﹣y=2与抛物线y2=4x交于A、B两点,则线段AB的中点坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com