证明:(1)如图,AH⊥面SBC,
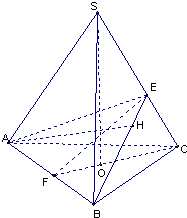
设BH交SC于E,连接AE
∵H是△SBC的垂心
∴BE⊥SC,
∵AH⊥平面SBC,SC⊆平面SBC
∴AH⊥SC,结合BE∩AH=H
∴SC⊥平面ABE,
∵AB⊆平面ABE,
∴AB⊥SC
设S在底面ABC内的射影为O,则SO⊥平面ABC,
∵AB⊆平面ABC
∴AB⊥SO,结合SC∩SO=S
∴AB⊥平面SCO,
∵CO⊆平面SCO
∴CO⊥AB,同理BO⊥AC,
可得O是△ABC的垂心
∵△ABC是正三角形
∴S在底面△ABC的射影O是△ABC的中心
∴三棱锥S-ABC为正三棱锥.…(6分)
(2)由(1)有SA=SB=SC=

,
延长CO交AB于F,连接EF
∵CF⊥AB,CF是EF在面ABC内的射影,
∴EF⊥AB,
∴∠EFC为二面角H-AB-C的平面角,∠EFC=30°,
∵SC⊥平面ABE,EF⊆平面ABE,
∴EF⊥SC,Rt△EFC中,∠ECF=60°,
可得Rt△SOC中,OC=SCcos60°=

,
SO=SCsin60°=3,
∴正三角形ABC中,AB=

OC=3,
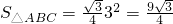
∴
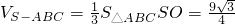
…(12分)
分析:(1)设BH交SC于E,连接AE,根据三垂线定理,结合BE⊥SC,得到AB⊥SC.再作出SO⊥平面ABC,结合三垂线定理的逆定理,得到CO⊥AB,同理BO⊥AC,可得O是△ABC的垂心,因为△ABC是正三角形,所以S在底面△ABC的射影O是正
△ABC的中心,最终得到三棱锥S-ABC为正三棱锥;
(2)延长CO交AB于F,连接EF,根据三垂线定理结合CF⊥AB,得到EF⊥AB,从而∠EFC即为二面角H-AB-C的平面角,从而在Rt△SOC中,∠ECF=90°-30°=60°,根据SC长结合三角函数的定义得到SO、CO的长,最后得到底面边长AB=3,求出底面三角形的面积,利用锥体体积公式可求出三棱锥S-ABC的体积.
点评:本题以一个正三棱锥的证明与计算为载体,考查了线面垂直的判定与性质、三垂线定理及其逆定理和二面角的平面角等知识,属于中档题.

 已知三棱锥S-ABC的底面是正三角形,A点在侧面SBC上的射影H是△SBC的垂心.
已知三棱锥S-ABC的底面是正三角形,A点在侧面SBC上的射影H是△SBC的垂心. ,求三棱锥S-ABC的体积.
,求三棱锥S-ABC的体积. 设BH交SC于E,连接AE
设BH交SC于E,连接AE ,
, ,
, OC=3,
OC=3,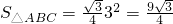
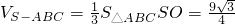 …(12分)
…(12分)
