
| A. | lna>-b-1 | B. | lna≥-b-1 | C. | lna≤-b-1 | D. | lna<-b-1 |
分析 由f(x)≥f(3),知x=3是函数f(x)的极值点,所以f′(3)=0,从而得到b=1-6a,作差:lna-(-b-1)=lna+2-6a,所以构造函数g(x)=lnx+2-6x,通过导数可求得g(x)≤g( $\frac{1}{6}$)<0,即g(x)<0,所以g(a)<0,所以lna<-b-1.
解答 解:f′(x)=2ax+b-$\frac{3}{x}$,
由题意可知,f(x)在x=3处取得最小值,
即x=3是f(x)的极值点;
∴f′(3)=0,∴6a+b=1,即b=1-6a;
作差,lna-(-b-1)=lna-6a+2,
令g(x)=lnx-6x+2,(x>0),则g′(x)=$\frac{1}{x}$-6=$\frac{1-6x}{x}$;
∴当0<x<$\frac{1}{6}$时,g′(x)>0,g(x)在(0,$\frac{1}{6}$)上单调递增;
当x>$\frac{1}{6}$时,g′(x)<0,g(x)在($\frac{1}{6}$,+∞)上单调递减;
∴g(x)≤g($\frac{1}{6}$)=1-ln6<0;
∴g(a)<0,即lna+b+1<0;
故lna<-b-1,
故选:D.
点评 考查最值的概念,极值的定义,函数导数符号和函数单调性的关系,通过构造函数比较两个式子大小的方法.


科目:高中数学 来源: 题型:选择题
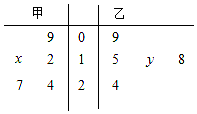 如图,茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x+y的值为( )
如图,茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x+y的值为( )| A. | 8 | B. | 10 | C. | 11 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{{5\sqrt{2}}}{8}$ | D. | $\frac{{\sqrt{2}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一条直线和一个圆 | B. | 一条直线和半个圆 | ||
| C. | 两条射线和一个圆 | D. | 一条线段和半个圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com