
【题目】某医院对治疗支气管肺炎的两种方案A,B进行比较研究,将志愿者分为两组,分别采用方案A和方案B进行治疗,统计结果如下:
有效 | 无效 | 合计 | |
使用方案A组 | 96 | 120 | |
使用方案B组 | 72 | ||
合计 | 32 |
(1)完成上述列联表,并比较两种治疗方案有效的频率;
(2)能否在犯错误的概率不超过0.05的前提下认为治疗是否有效与方案选择有关?
附: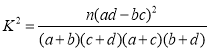 .
.
P( | 0.005 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】销售甲种商品所得利润是![]() 万元,它与投入资金
万元,它与投入资金![]() 万元的关系有经验公式
万元的关系有经验公式![]() ;销售乙种商品所得利润是
;销售乙种商品所得利润是![]() 万元,它与投入资金
万元,它与投入资金![]() 万元的关系有经验公式
万元的关系有经验公式![]() ,其中
,其中![]() ,
,![]() 为常数.现将3万元资金全部投入甲、乙两种商品的销售;若全部投入甲种商品,所得利润为
为常数.现将3万元资金全部投入甲、乙两种商品的销售;若全部投入甲种商品,所得利润为![]() 万元;若全部投入乙种商品,所得利润为1万元,若将3万元资金中的
万元;若全部投入乙种商品,所得利润为1万元,若将3万元资金中的![]() 万元投入甲种商品的销售,余下的投入乙种商品的销售,则所得利润总和为
万元投入甲种商品的销售,余下的投入乙种商品的销售,则所得利润总和为![]() 万元.
万元.
(1)求函数![]() 的解析式;
的解析式;
(2)怎样将3万元资金分配给甲、乙两种商品,才能使所得利润总和最大,并求最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 是圆心为
是圆心为![]() ,半径为1的圆.
,半径为1的圆.
(1)求曲线![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上的点,
上的点, ![]() 为曲线
为曲线![]() 上的点,求
上的点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出三个命题:①直线上有两点到平面的距离相等,则直线平行平面;②夹在两平行平面间的异面直线段的中点的连线平行于这个平面;③过空间一点必有唯一的平面与两异面直线平行.正确的是( )
A. ②③B. ①②C. ①②③D. ②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,
轴的非负半轴为极轴建立极坐标系, ![]() 点的极坐标为
点的极坐标为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)写出点![]() 的直角坐标及曲线
的直角坐标及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 的中点
的中点![]() 到直线
到直线![]() :
: ![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆![]() :
:![]() ,点
,点![]() 是圆
是圆![]() 内一个定点,点
内一个定点,点![]() 是圆上任意一点,线段
是圆上任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和半径
和半径![]() 相交于点
相交于点![]() .当点
.当点![]() 在圆上运动时,点
在圆上运动时,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.

(1)求曲线![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点(点
两点(点![]() 在
在![]() 两点之间).是否存在直线
两点之间).是否存在直线![]() 使得
使得![]() ?若存在,求直线
?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴,以相同的长度单位建立极坐标系.己知直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,曲线C的极坐标方程为
,曲线C的极坐标方程为![]() .
.
(1)设t为参数,若![]() ,求直线
,求直线![]() 的参数方程和曲线C的直角坐标方程;
的参数方程和曲线C的直角坐标方程;
(2)已知:直线![]() 与曲线C交于A,B两点,设
与曲线C交于A,B两点,设![]() ,且
,且![]() ,
,![]() ,
,![]() 依次成等比数列,求实数a的值.
依次成等比数列,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某地区2009年至2018年芯片产业投资额![]() (单位:亿元)的散点图,为了预测该地区2019年的芯片产业投资额,建立了
(单位:亿元)的散点图,为了预测该地区2019年的芯片产业投资额,建立了![]() 与时间变量
与时间变量![]() 的四个线性回归模型.根据2009年至2018年的数据建立模型①;根据2010年至2017年的数据建立模型②;根据2011年至2016年的数据建立模型③;根据2014年至2018年的数据建立模型④.则预测值更可靠的模型是( )
的四个线性回归模型.根据2009年至2018年的数据建立模型①;根据2010年至2017年的数据建立模型②;根据2011年至2016年的数据建立模型③;根据2014年至2018年的数据建立模型④.则预测值更可靠的模型是( )

A.①B.②C.③D.④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com