
【题目】设![]() 是大于1的自然数,找出所有自然数
是大于1的自然数,找出所有自然数![]() ,使得对于
,使得对于![]() 存在互质的自然数
存在互质的自然数![]() 、
、![]() ,满足
,满足![]() .
.
【答案】![]()
【解析】
先证明一个引理.
引理 设![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,且满足
,且满足![]() .若
.若![]() 是大于1的奇数,
是大于1的奇数, ![]() 是奇质数,则
是奇质数,则![]() 可以表示成
可以表示成![]() 的以自然数为指数的幂.
的以自然数为指数的幂.
引理的证明:设![]() 为
为![]() 、
、![]() 的最大公约数,可设
的最大公约数,可设![]() .由已知条件有
.由已知条件有![]() .
.
因此,存在某个非负整数![]() ,满足
,满足![]() .
.
由于![]() 是奇数,故有
是奇数,故有![]() .
.
用![]() 表示等式右端的数.由于
表示等式右端的数.由于![]() ,所以,
,所以,![]() 与
与![]() 中至少有一个大于1.而
中至少有一个大于1.而![]() ,因此,
,因此,![]() .由式①推出
.由式①推出![]() .
.
因为![]() 且
且![]() ,所以,它们都能被
,所以,它们都能被![]() 整除,且存在某个自然数
整除,且存在某个自然数![]() ,使得
,使得![]() .这样,
.这样,
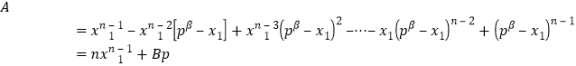 (
(![]() 是某个整数).
是某个整数).
因为![]() ,且
,且![]() ,于是
,于是![]() .
.
设![]() ,则
,则![]() ,即
,即![]() .
.
如果![]() ,同上面证明一样,可以证明
,同上面证明一样,可以证明![]() 可被
可被![]() 整除.如果
整除.如果![]() ,则
,则![]() ;这样重复下去,便可推出,存在某个自然数
;这样重复下去,便可推出,存在某个自然数![]() ,有
,有![]() .
.
下面证明本题的结论:![]() 的可能值只有2.
的可能值只有2.
设![]() ,其中
,其中![]() ,不妨设
,不妨设![]() .由于
.由于![]() ,
,![]() ,显然
,显然![]() 且
且![]() .讨论如下:
.讨论如下:
(1)若![]() 是偶数,则
是偶数,则![]() .
.
于是,![]() 不是3的整数次幂,矛盾.
不是3的整数次幂,矛盾.
(2)若![]() 是奇数,且
是奇数,且![]() ,则
,则![]() .于是,
.于是,![]() .以下证明
.以下证明![]() .
.
由引理知![]() .取
.取![]() ,代入后,可以认为
,代入后,可以认为![]() .于是,
.于是,![]() ,即证明
,即证明![]() .
.
由于![]() ,则
,则![]() .
.
因此,![]() .
.
于是,![]() 得证.
得证.
由![]() ,推出
,推出![]() .
.
而![]() 且
且![]() . ②
. ②
如果②中至少有一个不等号是严格不等号,那么,![]() .由
.由![]() 推出矛盾.可见,
推出矛盾.可见,![]() .
.
那么,![]() ,
,![]() 且
且![]() .故
.故![]() 是惟一满足条件的值.
是惟一满足条件的值.


 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:
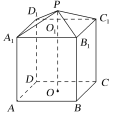
【题目】现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P-A1B1C1D1,下部的形状是正四棱柱ABCD-A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍,若AB=6 m,PO1=2 m,则仓库的容积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列事件:①任取这三条线段,这三条线段恰好组成直角三角形;②从一个三角形的三个顶点各任画一条射线,这三条射线交于一点;③实数![]() ,
,![]() 都不为,但
都不为,但![]() ;④明年12月28日的最高气温高于今年12月28日的最高气温.其中为随机事件的是( )
;④明年12月28日的最高气温高于今年12月28日的最高气温.其中为随机事件的是( )
A.①②③④B.①②④C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个![]() 的方格表的每个方格内填入1或
的方格表的每个方格内填入1或![]() ,如果任意一格内的数都等于与它有公共边的那些方格内所填数的乘积,则称这种填法是“成功”的.求“成功”填法的总数.
,如果任意一格内的数都等于与它有公共边的那些方格内所填数的乘积,则称这种填法是“成功”的.求“成功”填法的总数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若存在
,若存在![]() ,使
,使![]() 成立, 则称点
成立, 则称点![]() 为函数
为函数![]() 的不动点.
的不动点.
(1)若函数![]() 有不动点
有不动点![]() 和
和![]() , 求
, 求![]() 的值 ;
的值 ;
(2)若对于任意实数![]() ,函数
,函数![]() 总有 2 个相异的不动点 , 求实数
总有 2 个相异的不动点 , 求实数![]() 的取值范围;
的取值范围;
(3)若定义在实数集 R 上的奇函数![]() 存在(有限的)
存在(有限的)![]() 个不动点 , 求证:
个不动点 , 求证:![]() 必为奇数.
必为奇数.
查看答案和解析>>
科目:高中数学 来源: 题型:
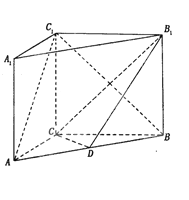
【题目】如图所示, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点,
(1)求证: AC1//平面CDB1;
(2)求二面角C1-AB-C的平面角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的方程为
的方程为![]() ,点
,点![]() 为坐标原点,点
为坐标原点,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,问是否存在实数
,问是否存在实数![]() 使得以
使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com