
已知数列{an}的通项公式为an = (nÎN*).
⑴求数列{an}的最大项;
⑵设bn = ,试确定实常数p,使得{bn}为等比数列;
⑶设 ,问:数列{an}中是否存在三项
,问:数列{an}中是否存在三项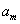 ,
,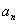 ,
, ,使数列
,使数列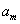 ,
,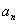 ,
, 是等差数列?如果存在,求出这三项;如果不存在,说明理由.
是等差数列?如果存在,求出这三项;如果不存在,说明理由.
解 ⑴由题意an = 2 + ,随着n的增大而减小,所以{an}中的最大项为a1 = 4.…4分
⑵bn = = = ,若{bn}为等比数列,
则b – bnbn+2= 0(nÎN* )所以 [(2 + p)3n+1 + ( 2 – p)]2 – [{2 + p)3n + (2 – p)][(2 + p)3n+2 + (2 – p)] = 0(nÎN*),
化简得(4 – p2)(2·3n+1 – 3n+2 – 3n ) = 0即– (4 – p2)·3n·4 = 0,解得p = ±2. ………………………7分
反之,当p = 2时,bn = 3n,{bn}是等比数列;当p = – 2时,bn = 1,{bn}也是等比数列.所以,当且仅当p = ±2时{bn}为等比数列. ………………………………………………………………10分
⑶因为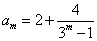 ,
,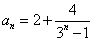 ,
,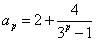 ,若存在三项
,若存在三项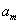 ,
,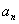 ,
,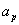 ,使数列
,使数列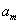 ,
,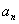 ,
,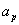 是等差数列,则
是等差数列,则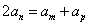 ,所以
,所以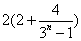 =
=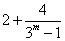
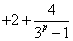 ,……………12分
,……………12分
化简得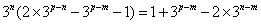 (*),因为
(*),因为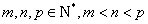 ,所以
,所以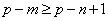 ,
,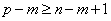 ,所以
,所以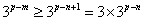 ,
,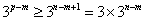 ,(*)的
,(*)的
左边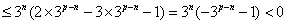 ,
,
右边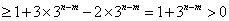 ,所以(*)式不可能成立,
,所以(*)式不可能成立,
故数列{an}中不存在三项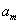 ,
,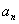 ,
,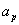 ,使数列
,使数列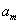 ,
,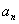 ,
,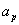 是等差数列. ……………16分
是等差数列. ……………16分


科目:高中数学 来源: 题型:
| 1 |
| Sn+n |
A、[
| ||||
B、(
| ||||
C、[
| ||||
D、[
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com