
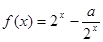 (
(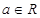 ),将
),将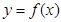 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数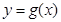 的图象,函数
的图象,函数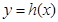 与函数
与函数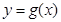 的图象关于直线
的图象关于直线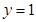 对称.
对称.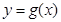 和
和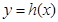 的解析式;
的解析式;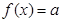 在
在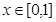 上有且仅有一个实根,求
上有且仅有一个实根,求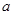 的取值范围;
的取值范围; ,已知
,已知 对任意的
对任意的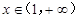 恒成立,求
恒成立,求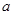 的取值范围.
的取值范围. 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
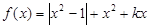 ,且定义域为(0,2).
,且定义域为(0,2).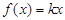 +3在(0,2)上的解;
+3在(0,2)上的解;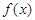 是定义域(0,2)上的单调函数,求实数
是定义域(0,2)上的单调函数,求实数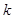 的取值范围;
的取值范围;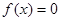 在(0,2)上有两个不同的解
在(0,2)上有两个不同的解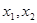 ,求k的取值范围。
,求k的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的方程
的方程 在
在 没有实数根,则
没有实数根,则 的取值范围是
的取值范围是
 与直线
与直线 有两个交点时,实数
有两个交点时,实数 的取值范围是
的取值范围是
 与点
与点 在直线
在直线 两侧, 则3b-2a>1;
两侧, 则3b-2a>1; 的图像向右平移
的图像向右平移 个单位后变为偶函数,则
个单位后变为偶函数,则 的最小值是
的最小值是 ;其中正确的结论是:__________________
;其中正确的结论是:__________________查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
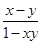 );当x∈(-1,0)时,有f(x)>0.若p=f(
);当x∈(-1,0)时,有f(x)>0.若p=f(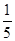 )+f(
)+f(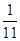 ),Q=f(
),Q=f(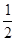 ),R=f(0);则 P,Q,R的大小关系为
),R=f(0);则 P,Q,R的大小关系为| A.R>Q>P | B.R>P>Q | C.P>R>Q | D.Q>P>R |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 销活动,当该商品的售价为
销活动,当该商品的售价为 元时,全年的促销费用为
元时,全年的促销费用为 万元;根据以往的销售经验,实施促销后的年销售量
万元;根据以往的销售经验,实施促销后的年销售量 万件,其中4
万件,其中4 为常数.当该商品的售价为6元时,年销售量为49万件.
为常数.当该商品的售价为6元时,年销售量为49万件. 的值;
的值; 万元与售价
万元与售价 元之间的关系;
元之间的关系;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com