
【题目】心理学研究表明,人极易受情绪的影响,某选手参加7局4胜制的兵乒球比赛.
(1)在不受情绪的影响下,该选手每局获胜的概率为![]() ;但实际上,如果前一句获胜的话,此选手该局获胜的概率可提升到
;但实际上,如果前一句获胜的话,此选手该局获胜的概率可提升到![]() ;而如果前一局失利的话,此选手该局获胜的概率则降为
;而如果前一局失利的话,此选手该局获胜的概率则降为![]() ,求该选手在前3局获胜局数
,求该选手在前3局获胜局数![]() 的分布列及数学期望;
的分布列及数学期望;
(2)假设选手的三局比赛结果互不影响,且三局比赛获胜的概率为![]() ,记
,记![]() 为锐角
为锐角![]() 的内角,求证:
的内角,求证:![]()
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】某市食品药品监督管理局开展2020年春季快递餐饮安全检查,对本市的8个快递配餐点进行了原料采购加工标准和卫生标准的检查和评分,其评分情况如表所示:
快递配餐点编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
原料采购加工标准评分 | 82 | 75 | 70 | 66 | 83 | 93 | 95 | 100 |
卫生标准评分 | 81 | 79 | 77 | 75 | 82 | 83 | 84 | 87 |
(1)已知![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(精确到0.1)
的线性回归方程;(精确到0.1)
(2)现从8个被检查点中任意抽取两个组成一组,若两个点的原料采购加工标准和卫生标准的评分均超过80分,则组成“快递标兵配餐点”,求该组被评为“快递标兵配餐点”的概率.
参考公式: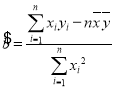 ,
,![]() ;参考数据:
;参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有![]() 个小球,甲、乙两位同学轮流且不放回抓球,每次最少抓1个球,最多抓3个球,规定谁抓到最后一个球谁赢. 如果甲先抓,那么下列推断正确的是( )
个小球,甲、乙两位同学轮流且不放回抓球,每次最少抓1个球,最多抓3个球,规定谁抓到最后一个球谁赢. 如果甲先抓,那么下列推断正确的是( )
A. 若![]() =4,则甲有必赢的策略 B. 若
=4,则甲有必赢的策略 B. 若![]() =6,则乙有必赢的策略
=6,则乙有必赢的策略
C. 若![]() =9,则甲有必赢的策略 D. 若
=9,则甲有必赢的策略 D. 若![]() =11,则乙有必赢的策略
=11,则乙有必赢的策略
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点.
上一点.
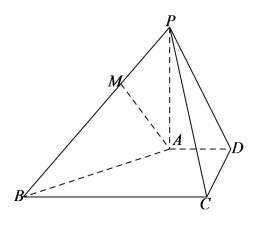
(I)若![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
(II)若![]() ,
,![]() ,异面直线
,异面直线![]() 与
与![]() 成
成![]() 角,二面角
角,二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的长及直线
的长及直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产的产品中分正品与次品,正品重![]() ,次品重
,次品重![]() ,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第
,现有5袋产品(每袋装有10个产品),已知其中有且只有一袋次品(10个产品均为次品)如果将5袋产品以1~5编号,第![]() 袋取出
袋取出![]() 个产品(
个产品(![]() ),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量
),并将取出的产品一起用秤(可以称出物体重量的工具)称出其重量![]() ,若次品所在的袋子的编号是2,此时的重量
,若次品所在的袋子的编号是2,此时的重量![]() _________
_________![]() ;若次品所在的袋子的编号是
;若次品所在的袋子的编号是![]() ,此时的重量
,此时的重量![]() _______
_______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了了解强度![]() (单位:分贝)与声音能量
(单位:分贝)与声音能量![]() (单位:
(单位:![]() )之间的关系,将测量得到的声音强度
)之间的关系,将测量得到的声音强度![]() 和声音能量
和声音能量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.

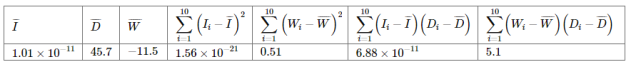
表中![]() ,
,![]()
(1)根据表中数据,求声音强度![]() 关于声音能量
关于声音能量![]() 的回归方程
的回归方程![]() ;
;
(2)当声音强度大于60分贝时属于噪音,会产生噪声污染,城市中某点![]() 共受到两个声源的影响,这两个声源的声音能量分别是
共受到两个声源的影响,这两个声源的声音能量分别是![]() 和
和![]() ,且
,且![]() .已知点
.已知点![]() 的声音能量等于声音能量
的声音能量等于声音能量![]() 与
与![]() 之和.请根据(1)中的回归方程,判断
之和.请根据(1)中的回归方程,判断![]() 点是否受到噪声污染的干扰,并说明理由.
点是否受到噪声污染的干扰,并说明理由.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: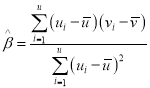 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com