定义F(x,y)=(1+x)y,其中x,y∈(0,+∞).
(1)令函数f(x)=F(1,log2(x3+ax2+bx+1)),其图象为曲线C,若存在实数b使得曲线C在x(-4<x<-1)处有斜率为-8的切线,求实数a的取值范围;
(2)令函数g(x)=F(1,log2[(lnx-1)ex+x]),是否存在实数x∈[1,e],使曲线y=g(x)在点x=x处的切线与y轴垂直?若存在,求出x的值;若不存在,请说明理由.
(3)当x,y∈N,且x<y时,求证:F(x,y)>F(y,x).
【答案】
分析:(1)先求出f(x)的解析式,设曲线C在x
(-4<x
<-1)处有斜率为-8的切线,建立等式,根据log
2(x
3+ax
2+bx+1)>0消去b得-2

-ax
-8<0,使得2x
2+ax
+8>0 在-4<x
<-1有解,求出a的取值范围即可;
(2)先求g′(x)=(

+lnx-1)e
x+1,令h(x)=

+lnx-1,然后利用导数研究h(x)在区间[1,e]上的最小值,从而求出g′(x
)的取值范围,曲线y=g(x)在点x=x
处的切线与y轴垂直等价于方程g′(x
)=0有实数解,而g′(x
)>0,即方程g′(x
)=0无实数解,从而得到结论;
(3)令h(x)=

,x≥1,则h′(x)=

,令p(x)=

-ln(1+x),x≥0,利用导数研究p(x)在[0,+∞)上的单调性,从而得到函数h(x)在[1,+∞)上的单调性,即可证得结论.
解答:解:(1)f(x)=F(1,log
2(x
3+ax
2+bx+1))=x
3+ax
2+bx+1,
设曲线C在x
(-4<x
<-1)处有斜率为-8的切线,
又由题设知log
2(x
3+ax
2+bx+1)>0,f′(x)=3x
2+2ax+b,3x
2+2ax
+b=-8 ①
∴存在实数b使得-4<x
<-1 ②有解,(3分)
x
3+ax
2+bx
>0 ③
由①得b=-8-3
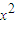
-2ax
,代入③得-2

-ax
-8<0,
∴由 2x
2+ax
+8>0 在-4<x
<-1有解,
得2×(-4)
2+a×(-4)+8>0或2×(-1)
2+a×(-1)+8>0,
∴a<10或a<10,∴a<10、(5分)
(2)∵g(x)=(lnx-1)e
x+x,
∴g′(x)=(lnx-1)′e
x+(lnx-1)(e
x)′+1=

+(lnx-1)e
x+1=(

+lnx-1)e
x+1.(6分)
设h(x)=

+lnx-1、则h′(x)=-

+

=

,
当x∈[1,e]时,h′(x)≥0.
h(x)为增函数,因此h(x)在区间[1,e]上的最小值为ln1=0,即

+lnx-1≥0.
当x
∈[1,e]时,ex
>0,

+lnx
-1≥0,
∴g′(x
)=(

+lnx
-1)ex
+1≥1>0.(8分)
曲线y=g(x)在点x=x
处的切线与y轴垂直等价于方程g′(x
)=0有实数解,
而g′(x
)>0,即方程g′(x
)=0无实数解.
故不存在实数x
∈[1,e],使曲线y=g(x)在点x=x
处的切线与y轴垂直.(9分)
(3)证明:令h(x)=

,x≥1,由h′(x)=

,
又令p(x)=

-ln(1+x),x≥0,
∴p′(x)=

-

=

≤0,
∴p(x)在[0,+∞)上单调递减,
∴当x>0时,有p(x)<p(0)=0,
∴当x≥1时,有h′(x)<0,
∴h(x)在[1,+∞)上单调递减,(11分)
∴当1≤x<y时,有

>

,
∴yln(1+x)>xln(1+y),∴(1+x)
y>(1+y)
x,
∴当x,y∈N
?,且x<y时,F(x,y)>F(y,x).(13分)
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及利用导数求闭区间上函数的最值,同时考查了转化的数学思想,属于中档题.

 -ax-8<0,使得2x2+ax+8>0 在-4<x<-1有解,求出a的取值范围即可;
-ax-8<0,使得2x2+ax+8>0 在-4<x<-1有解,求出a的取值范围即可; +lnx-1)ex+1,令h(x)=
+lnx-1)ex+1,令h(x)= +lnx-1,然后利用导数研究h(x)在区间[1,e]上的最小值,从而求出g′(x)的取值范围,曲线y=g(x)在点x=x处的切线与y轴垂直等价于方程g′(x)=0有实数解,而g′(x)>0,即方程g′(x)=0无实数解,从而得到结论;
+lnx-1,然后利用导数研究h(x)在区间[1,e]上的最小值,从而求出g′(x)的取值范围,曲线y=g(x)在点x=x处的切线与y轴垂直等价于方程g′(x)=0有实数解,而g′(x)>0,即方程g′(x)=0无实数解,从而得到结论; ,x≥1,则h′(x)=
,x≥1,则h′(x)= ,令p(x)=
,令p(x)= -ln(1+x),x≥0,利用导数研究p(x)在[0,+∞)上的单调性,从而得到函数h(x)在[1,+∞)上的单调性,即可证得结论.
-ln(1+x),x≥0,利用导数研究p(x)在[0,+∞)上的单调性,从而得到函数h(x)在[1,+∞)上的单调性,即可证得结论.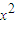 -2ax,代入③得-2
-2ax,代入③得-2 -ax-8<0,
-ax-8<0, +(lnx-1)ex+1=(
+(lnx-1)ex+1=( +lnx-1)ex+1.(6分)
+lnx-1)ex+1.(6分) +lnx-1、则h′(x)=-
+lnx-1、则h′(x)=- +
+ =
= ,
, +lnx-1≥0.
+lnx-1≥0. +lnx-1≥0,
+lnx-1≥0, +lnx-1)ex+1≥1>0.(8分)
+lnx-1)ex+1≥1>0.(8分) ,x≥1,由h′(x)=
,x≥1,由h′(x)= ,
, -ln(1+x),x≥0,
-ln(1+x),x≥0, -
- =
= ≤0,
≤0, >
> ,
,

 期末集结号系列答案
期末集结号系列答案