
【题目】已知![]() 为圆
为圆![]() 上的动点,
上的动点, ![]() ,
,![]() 为定点,
为定点,
(1)求线段![]() 中点M的轨迹方程;
中点M的轨迹方程;
(2)若![]() ,求线段
,求线段![]() 中点N的轨迹方程.
中点N的轨迹方程.
科目:高中数学 来源: 题型:
【题目】某单位每天的用电量![]() (度)与当天最高气温
(度)与当天最高气温![]() (℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
(℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
最高气温(℃) | 26 | 29 | 31 | 34 |
用电量 (度) | 22 | 26 | 34 | 38 |
(Ⅰ)根据表中数据,求出回归直线的方程![]() (其中
(其中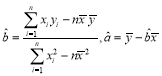 );
);
(Ⅱ)试预测某天最高气温为33℃时,该单位当天的用电量(精确到1度).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,
,![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() ,
,![]() .
.
(1)若![]() 为等边三角形,求椭圆
为等边三角形,求椭圆![]() 的方程;
的方程;
(2)若椭圆![]() 的短轴长为2,过点
的短轴长为2,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】重庆因夏长酷热多伏旱而得名“火炉”,八月是重庆最热、用电量最高的月份.下图是沙坪坝区居民八月份用电量(单位:度)的频率分布直方图,其分组区间依次为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直方图中的![]() ;
;
(2)根据直方图估计八月份用电量的众数和中位数;
(3)在用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取11户居民,则用电量在
的四组用户中,用分层抽样的方法抽取11户居民,则用电量在![]() 的用户应抽取多少户?
的用户应抽取多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com