
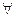 x∈R,r(x)与s(x)有且仅有一个是真命题.求实数m的取值范围.
x∈R,r(x)与s(x)有且仅有一个是真命题.求实数m的取值范围.科目:高中数学 来源:不详 题型:解答题
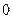 不能作除数;
不能作除数;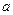 ,
,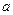 不能取对数;
不能取对数;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
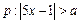 和条件
和条件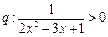 ,现在要选择适当的实数
,现在要选择适当的实数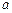 的值,分别利用所给的两上条件作为
的值,分别利用所给的两上条件作为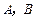 构造命题:“若
构造命题:“若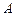 则
则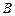 ”,并使得构造的原命题为真命题,而其逆命题为假命题,则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
”,并使得构造的原命题为真命题,而其逆命题为假命题,则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
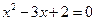 ,则
,则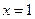 或
或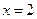 ;②若
;②若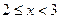 ,则
,则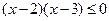 ;
;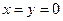 ,则
,则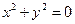 ;
;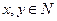 ,且
,且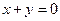 是奇数,则
是奇数,则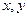 中一个是奇数,一个是偶数,那么( ).
中一个是奇数,一个是偶数,那么( ).| A.①的逆命题为真 | B.②的否命题为真 |
| C.③的否命题为假 | D.④的逆命题为假 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
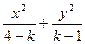 =1,给出下面四个命题:
=1,给出下面四个命题: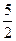
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
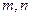 是两条不同的直线,
是两条不同的直线,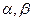 是两个不同的平面,给出下列四个命题:
是两个不同的平面,给出下列四个命题: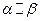 ,
,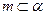 ,则
,则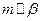 ; 2)若
; 2)若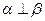 ,
,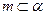 ,则
,则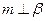 ;
;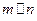 ,
,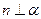 ,则
,则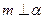 ;4)若
;4)若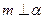 ,
,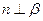 ,
,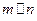 ,则
,则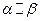 .
.| A.3 | B. 2 | C. 1 | D.0 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
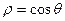 与直线
与直线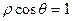 相切;
相切;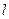 的参数方程为
的参数方程为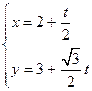
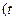 为参数),则它的倾斜角为
为参数),则它的倾斜角为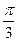 ;
;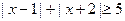 的解集为
的解集为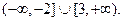
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com