
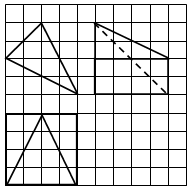
 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则它的体积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则它的体积为( )| A. | 48 | B. | 16 | C. | 32 | D. | 16$\sqrt{5}$ |
分析 根据三视图画出此几何体:镶嵌在正方体中的四棱锥,由正方体的位置关系判断底面是矩形,做出四棱锥的高后,利用线面垂直的判定定理进行证明,由等面积法求出四棱锥的高,利用椎体的体积公式求出答案.
解答 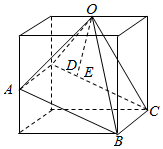 解:根据三视图得出:该几何体是镶嵌在正方体中的四棱锥O-ABCD,
解:根据三视图得出:该几何体是镶嵌在正方体中的四棱锥O-ABCD,
正方体的棱长为4,O、A、D分别为棱的中点,
∴OD=2$\sqrt{2}$,AB=DC=OC=2$\sqrt{5}$,
做OE⊥CD,垂足是E,
∵BC⊥平面ODC,∴BC⊥OE、BC⊥CD,则四边形ABCD是矩形,
∵CD∩BC=C,∴OE⊥平面ABCD,
∵△ODC的面积S=$4×4-\frac{1}{2}×2×2-\frac{1}{2}×2×4×2$=6,
∴6=$\frac{1}{2}•CD•OE$=$\frac{1}{2}×2\sqrt{5}×OE$,得OE=$\frac{6}{\sqrt{5}}$,
∴此四棱锥O-ABCD的体积V=$\frac{1}{3}{S}_{矩形ABCD}•OE$=$\frac{1}{3}×4×2\sqrt{5}×\frac{6}{\sqrt{5}}$=16,
故选:B.
点评 本题考查三视图求不规则几何体的体积,以及等面积法的应用,由三视图正确复原几何体、并放在对应的正方体中是解题的关键,考查空间想象能力和数形结合思想.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m<-2或m>-1 | B. | -2<m<0 | C. | -2<m<-1 | D. | m>-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,5,2) | B. | (3,-5,2) | C. | (3,-5,-2) | D. | (-3,-5,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5$\sqrt{15}$π | B. | 60π | C. | 60$\sqrt{15}$π | D. | 20$\sqrt{15}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com