练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知△ABC为锐角三角形，向量m＝(3cos2A，sin A)，n＝(1，－sin A)，且m⊥n.

    (1)求A的大小；

    (2)当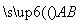＝pm，＝qn(p>0，q>0)，且满足p＋q＝6时，求△ABC面积的最大值．


    解　(1)∵m⊥n，∴3cos2A－sin2A＝0.

    ∴3cos2A－1＋cos2A＝0，∴cos2A＝.

    又∵△ABC为锐角三角形，

    ∴cos A＝，∴A＝.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    奇函数f(x)的定义域为R.若f(x＋2)为偶函数，且f(1)＝1，则f(8)＋f(9)＝(　　)

    A．－2  　　B．－1 　　 C．0  　　　D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设D，E分别是△ABC的边AB，BC上的点，AD＝AB，BE＝BC.若(λ1，λ2为实数)，则λ1＋λ2的值为________．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知各项全不为零的数列{an}的前n项和为Sn，Sn＝，n∈N*.

    (1)求证：数列{an}为等差数列；

    (2)若a2＝3，求证：当n∈N*时，＋＋…＋<.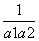

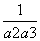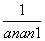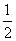    查看答案和解析>>

    科目：高中数学 来源： 题型：


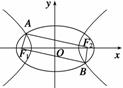    如图，F1，F2是椭圆C1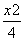：＋y2＝1与双曲线C2的公共焦点，A，B分别是C1，C2在第二、四象限的公共点．若四边形AF1BF2为矩形，则C2的离心率是(　　)

    A.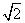  B.  C.  D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝，则f(2＋log23)的值为(　　)

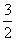    A.  B.  C.  D.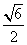

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若直线l与曲线C满足下列两个条件：

    (1)直线l在点P(x0，y0)处与曲线C相切；

    (2)曲线C在点P附近位于直线l的两侧，则称直线l在点P处“切过”曲线C.

    下列命题正确的是________(写出所有正确命题的编号)．

    ①直线l：y＝0在点P(0,0)处“切过”曲线C：y＝x3；

    ②直线l：x＝－1在点P(－1,0)处“切过”曲线C：y＝(x＋1)3；

    ③直线l：y＝x在点P(0,0)处“切过”曲线C：y＝sin x；

    ④直线l：y＝x在点P(0,0)处“切过”曲线C：y＝tan x；

    ⑤直线l：y＝x－1在点P(1,0)处“切过”曲线C：y＝ln x.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给出下列四个对象：（1）某城市的大胖子；（2）你所在班中身高超过1.80米的同学；（3）第30届奥运会中的所有比赛项目；（4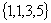）.其中能构成集合的个数为（   ）

    A．1        B．2        C．3        D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    二次函数在区间上的最大值为，则的值为       

    查看答案和解析>>

    同步练习册答案