
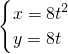 (t为参数),圆C2的极坐标方程为ρ=r(r>0),若斜率为1的直线经过抛物线C1的焦点,且与圆C2相切,则r=________.
(t为参数),圆C2的极坐标方程为ρ=r(r>0),若斜率为1的直线经过抛物线C1的焦点,且与圆C2相切,则r=________.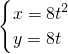 (t为参数),则普通方程为y2=8x,焦点坐标为(2,0);圆C2的极坐标方程为ρ=r(r>0),表示以原点为圆心,r为半径的圆
(t为参数),则普通方程为y2=8x,焦点坐标为(2,0);圆C2的极坐标方程为ρ=r(r>0),表示以原点为圆心,r为半径的圆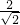 =
=

 .
.

科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 3 |
|
| π |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 A.(不等式选讲选做题)如果存在实数x使不等式|x+1|-|x-2|<k成立,则实数k的取值范围是
A.(不等式选讲选做题)如果存在实数x使不等式|x+1|-|x-2|<k成立,则实数k的取值范围是| 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年陕西省宝鸡市金台区高三(上)11月质量检测数学试卷(文科)(解析版) 题型:填空题
 ,则线段CD的长为 .
,则线段CD的长为 .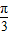 )的直角坐标是 .
)的直角坐标是 .
查看答案和解析>>
科目:高中数学 来源:2011年陕西省西安市五大名校高考数学一模试卷(文科)(解析版) 题型:解答题
 ,则AC的长为 .
,则AC的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com