
已知二次函数 f(x)=ax2+bx+1(a,b∈R,a>0),设方程f(x)=x的两实数根为x1,x2.
(1)如果x1<2<x2<4,设函数f(x)的对称轴为x=x0,求证x0>-1;
(2)如果|x1|<2,|x2-x1|=2,求b的取值范围.
(1)证明略 (2) 当0<x1<2时,b<![]() ,当-2<x1<0时,b>
,当-2<x1<0时,b>![]() .
.
(1)设g(x)=f(x)-x=ax2+(b-1)x+1,且x>0.
∵x1<2<x2<4,∴(x1-2)(x2-2)<0,即x1x2<2(x1+x2)-4,
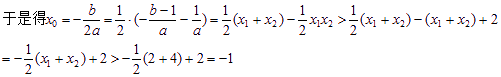
(2)解:由方程g(x)=ax2+(b-1)x+1=0可知x1·x2=![]() >0,所以x1,x2同号?
>0,所以x1,x2同号?
1°若0<x1<2,则x2-x1=2,∴x2=x1+2>2,
∴g(2)<0,即4a+2b-1<0 ①
又(x2-x1)2=![]()
∴2a+1=![]() (∵a>0)代入①式得,
(∵a>0)代入①式得,
2![]() <3-2b ②
<3-2b ②
解②得b<![]()
2°若 -2<x1<0,则x2=-2+x1<-2
∴g(-2)<0,即4a-2b+3<0 ③
又2a+1=![]() ,代入③式得
,代入③式得
2![]() <2b-1 ④
<2b-1 ④
解④得b>![]() .
.
综上,当0<x1<2时,b<![]() ,当-2<x1<0时,b>
,当-2<x1<0时,b>![]() .
.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| x |
| 1 |
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| bx-1 | a2x+2b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| bx-1 | a2x+2b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com