
一圆和直线l:x+2y-3=0切于点P(1,1),且半径为5,求这个圆的方程.
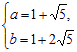 或
或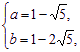
利用直线与圆相切列方程,求出方程中的常参数.
解法一:设圆心坐标为C(a,b),
圆方程即为(x-a)2+(y-b)2=25.
∵点P(1,1)在圆上,
则(1-a)2+(1-b)2=25. ①
又l为圆C的切线,
则CP⊥l,∴![]() =2. ②
=2. ②
联立①②解得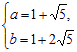 或
或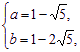
即所求圆的方程是(x-1-![]() )2+(y-1-2
)2+(y-1-2![]() )2=25
)2=25
或(x-1+![]() )2+(y-1+2
)2+(y-1+2![]() )2=25.
)2=25.
解法二:设圆方程为(x-a)2+(y-b)2=25,
过P(1,1)的切线方程是(1-a)(x-a)+(1-b)(y-b)=25.
整理得(1-a)x+(1-b)y-[a(1-a)+b(1-b)+25]=0.
这就是已知直线l的方程,
即![]() =
=![]() =
=![]() .
.
解得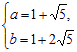 或
或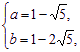
即得圆方程.
注:当然还有很多方法,比如利用圆的一般方程x2+y2+Dx+Ey+F=0来求解也可.


科目:高中数学 来源: 题型:
| PC |
| 1 |
| 2 |
| PQ |
| PC |
| 1 |
| 2 |
| PQ |
| PE |
| PF |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | m |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年安徽省芜湖一中高二(上)数学寒假作业(必修2)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2009-2010学年福建省三明市大田一中高二(上)数学寒假作业(必修2)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com