Question

6．已知正方体ABCD一A₁B₁C₁D₁，下列命题：
①（ $\overrightarrow{{A}_{1}A}$+$\overrightarrow{{A}_{1}{D}_{1}}$+$\overrightarrow{{A}_{1}{B}_{1}}$）²=3$\overrightarrow{{A}_{1}{B}_{1}}$²，
②$\overrightarrow{{A}_{1}C}$•（$\overrightarrow{{A}_{1}{B}_{1}}$-$\overrightarrow{{A}_{1}A}$）=0
③向量$\overrightarrow{A{D_1}}$与向量$\overrightarrow{{A_1}B}$的夹角为60°
④正方体ABCD一A₁B₁C₁D₁的体积为$|\overrightarrow{AB}•\overrightarrow{A{A_1}}•\overrightarrow{AD}|$，
其中正确命题序号是（　　）

• A． ①②
• B． ①②③
• C． ①④
• D． ①②④

Answer 1

分析 利用正方体的性质，建立空间直角坐标系，得到相关向量的坐标，利用坐标运算得到正确选项．

解答 解：建立空间直角坐标系，如图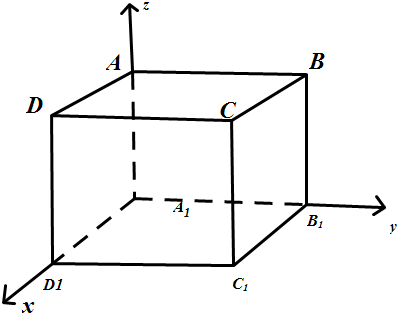
$\overrightarrow{{A}_{1}A}$=（0，0，1），$\overrightarrow{{A}_{1}{D}_{1}}$=（1，0，0，），$\overrightarrow{{A}_{1}{B}_{1}}$=（0，1，0），$\overrightarrow{{A}_{1}C}$=（1，1，1），$\overrightarrow{A{D}_{1}}$=（1，0，-1），
所以对于①（ $\overrightarrow{{A}_{1}A}$+$\overrightarrow{{A}_{1}{D}_{1}}$+$\overrightarrow{{A}_{1}{B}_{1}}$）²=（1，1，1）²=3=3$\overrightarrow{{A}_{1}{B}_{1}}$²，故①正确；
对于②$\overrightarrow{{A}_{1}C}$•（$\overrightarrow{{A}_{1}{B}_{1}}$-$\overrightarrow{{A}_{1}A}$）=（1，1，1）（0，1，-1）=0；故②正确；
对于③，Y因为$\overrightarrow{A{D}_{1}}•\overrightarrow{{A}_{1}B}$=（1，0，-1）（0，1，1）=-1，向量$\overrightarrow{A{D_1}}$与向量$\overrightarrow{{A_1}B}$的夹角为120°；故③错误；
④正方体ABCD一A₁B₁C₁D₁的体积为$|\overrightarrow{AB}||\overrightarrow{A{A}_{1}}||\overrightarrow{AD}|$，但是$|\overrightarrow{AB}•\overrightarrow{A{A_1}}•\overrightarrow{AD}|$=0，故④错误．
故选：A

点评 本题考查了正方体性质定义域以及向量的坐标运算，考查学生的空间想象能力，属于基础题．