
若函数f(x)=2sin(ωx+φ),x∈R(其中ω>0,|φ|<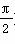 )的最小正周期是π,且f(0)=
)的最小正周期是π,且f(0)=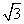 ,则( ).
,则( ).
A.ω=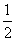 ,φ=
,φ=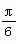 B.ω=
B.ω=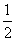 ,φ=
,φ=
C.ω=2,φ=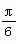 D.ω=2,φ=
D.ω=2,φ=
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f′(x)的图象经过(1,0),(2,0)点,如图所示.

(1)求x0的值;
(2)求a,b,c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=2sin(ωx+φ),x∈R,其中ω>0,-π<φ≤π.若f(x)的最小正周期为6π,且当x=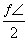 时,f(x)取得最大值,则( )
时,f(x)取得最大值,则( )
A.f(x)在区间[-2π,0]上是增函数
B.f(x)在区间[-3π,-π]上是增函数
C.f(x)在区间[3π,5π]上是减函数
D.f(x)在区间[4π,6π]上是减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
将函数y=sin(ωx+φ) 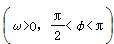 的图象,向右最少平移
的图象,向右最少平移 个单位长度,或向左最少平移
个单位长度,或向左最少平移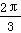 个单位长度,所得到的函数图象均关于原点中心对称,则ω=________.
个单位长度,所得到的函数图象均关于原点中心对称,则ω=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
函数f(x)=Asin(ωx+φ)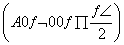 的部分图象如图所示.
的部分图象如图所示.
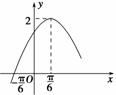
(1)求f(x)的解析式;
(2)设g(x)= ,求函数g(x)在x∈
,求函数g(x)在x∈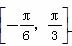 上的最大值,并确定此时x的值.
上的最大值,并确定此时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)①证明两角和的余弦公式
C(α+β):cos(α+β)=cos αcos β-sin αsin β;
②由C(α+β)推导两角和的正弦公式
S(α+β):sin(α+β)=sin αcos β+cos αsin β.
(2)已知cos α=-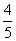 ,
,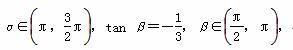 ,
,
求cos(α+β).
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列命题:
①向量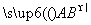 的长度与向量
的长度与向量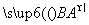 的长度相等;
的长度相等;
②向量a与b平行,则a与b的方向相同或相反;
③两个有共同起点而且相等的向量,其终点必相同;
④两个有公共终点的向量,一定是共线向量;
⑤向量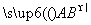 与向量
与向量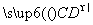 是共线向量,则点A、B、C、D必在同一条直线上.
是共线向量,则点A、B、C、D必在同一条直线上.
其中不正确的个数为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com