Question

如图，边长为2的正方形所在的平面与平面垂直，与的交点为， ，且.

（1）求证：平面；

（2）求直线与平面所成线面角的正切值.

 

Answer 1

（1）见解析；（2）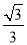

【解析】

试题分析：(1)证明线面垂直的方法：一是线面垂直的判定定理；二是利用面面垂直的性质定理；三是平行线法（若两条平行线中的一条垂直于这个平面，则另一条也垂直于这个平面.解题时，注意线线、线面与面面关系的相互转化.(2)求直线与平面所成的角，关键是利用定义作出直线和平面所成的角，必要时，可利用平行线与同一个平面所成的角相等，平移直线位置，以方便寻找直线在该平面的射影

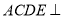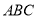试题解析：(1) ∵平面平面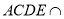,平面平面,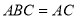

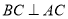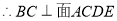, 2分

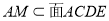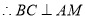又, 3分

∵四边形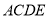是正方形 ，，

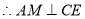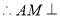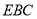平面． 5分

(2) 取AB的中点F,连结CF,EF.

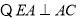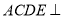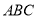,平面平面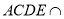,平面平面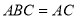

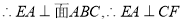6分

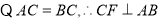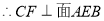又, 7分

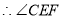即为直线EC与平面ABE所成角。 ..8分

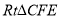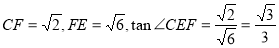在中， 10分

考点：（1）证明线面垂直（2）求直线与平面所成的角