
”¾ĢāÄæ”ææēÄźÓŠĀĮŖ»¶Ķķ»į¼ņ³ĘæēÄźĶķ»į£¬ŹĒÖøĆæÄźŃōĄśÄźÄ©12ŌĀ31ČÕĶķÉĻø÷µēŹÓĢØŗĶÕžø®ĪŖĻ²ÓŠĀ¶ų¾«ŠÄ²ß»®µÄŃŻ³Ŗ»į»ī¶Æ£¬æēÄźĶķ»įŹ×“Ī³öĻÖŌŚøŪĢصŲĒų£¬æēÄźĶķ»įŅņŠĪŹ½ŗĶ¾Ł°ģµŲ²»Ķ¬Ņņ¶ųĆū³ĘŅ²²»Ķ¬£¬ČēŃėŹÓĘōŗ½2020æēÄźŹ¢µä£¬ŗžÄĻĪĄŹÓæēğѯ³Ŗ»į£¬¶«·½ĪĄŹÓÓŠĀĶķ»įµČ.ijµēŹÓĢØĪŖĮĖĮĖ½ā2020Äź¾Ł°ģµÄæēÄźÓŠĀĶķ»į¹ŪÖŚµÄĀśŅā¶Č£¬ĻÖ·Ö±šĖ껜є³ö![]() Ćū¹ŪÖŚ¶ŌÓŠĀĶķ»įµÄÖŹĮæĘĄ¹ĄĘĄ·Ö£¬×īøß·ÖĪŖ
Ćū¹ŪÖŚ¶ŌÓŠĀĶķ»įµÄÖŹĮæĘĄ¹ĄĘĄ·Ö£¬×īøß·ÖĪŖ![]() ·Ö£¬×ŪŗĻµĆ·ÖĒéæöČēĻĀ±ķĖłŹ¾£ŗ
·Ö£¬×ŪŗĻµĆ·ÖĒéæöČēĻĀ±ķĖłŹ¾£ŗ
×ŪŗĻµĆ·Ö |
|
|
|
|
|
|
|
¹ŪÖŚČĖŹż | 5 | 10 | 25 | 30 | 15 | 10 | 5 |
øł¾Ż±ķÖŠµÄŹż¾Ż£¬»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©øł¾Ż±ķÖŠµÄŹż¾Ż£¬»ęÖĘÕā![]() Ī»¹ŪÖŚ“ņ·ÖµÄʵĀŹ·Ö²¼Ö±·½Ķ¼£»
Ī»¹ŪÖŚ“ņ·ÖµÄʵĀŹ·Ö²¼Ö±·½Ķ¼£»
£Ø2£©ŅŃÖŖ¹ŪÖŚµÄĘĄ·Ö![]() ½üĖĘ·ž“Ó
½üĖĘ·ž“Ó![]() £¬ĘäÖŠ
£¬ĘäÖŠ![]() ŹĒ·“Ó¦Ė껜±äĮæ
ŹĒ·“Ó¦Ė껜±äĮæ![]() ȔֵµÄĘ½¾łĖ®Ę½µÄĢŲÕ÷Źż£¬¹¤×÷ČĖŌ±ŌŚ·ÖĪöŹż¾ŻŹ±·¢ĻÖ£¬æÉÓĆ
ȔֵµÄĘ½¾łĖ®Ę½µÄĢŲÕ÷Źż£¬¹¤×÷ČĖŌ±ŌŚ·ÖĪöŹż¾ŻŹ±·¢ĻÖ£¬æÉÓĆ![]() Ī»¹ŪÖŚĘĄ·ÖµÄĘ½¾łŹż¹Ą¼Ę
Ī»¹ŪÖŚĘĄ·ÖµÄĘ½¾łŹż¹Ą¼Ę![]() £¬µ«ÓÉÓŚĘĄ·Ö¹ŪÖŚČĖŹż½ĻÉŁ£¬Īó²ī½Ļ“ó£¬ĖłŅŌ²»ÄÜÖ±½ÓÓĆ
£¬µ«ÓÉÓŚĘĄ·Ö¹ŪÖŚČĖŹż½ĻÉŁ£¬Īó²ī½Ļ“ó£¬ĖłŅŌ²»ÄÜÖ±½ÓÓĆ![]() Ī»¹ŪÖŚĘĄ·ÖµÄ±ź×¼²īµÄÖµ¹Ą¼Ę
Ī»¹ŪÖŚĘĄ·ÖµÄ±ź×¼²īµÄÖµ¹Ą¼Ę![]() £¬¶ųŌŚÕā
£¬¶ųŌŚÕā![]() Ī»¹ŪÖŚ“ņ·ÖµÄʵĀŹ·Ö²¼Ö±·½Ķ¼µÄ»ł“”ÉĻŅĄ¾Ż
Ī»¹ŪÖŚ“ņ·ÖµÄʵĀŹ·Ö²¼Ö±·½Ķ¼µÄ»ł“”ÉĻŅĄ¾Ż![]() Ą“¹Ą¼Ę
Ą“¹Ą¼Ę![]() øüæĘѧŗĻĄķ£¬ŹŌĒó
øüæĘѧŗĻĄķ£¬ŹŌĒó![]() ŗĶ
ŗĶ![]() µÄ¹Ą¼ĘÖµ£Ø
µÄ¹Ą¼ĘÖµ£Ø![]() µÄ½į¹ū¾«Č·µ½Š”ŹżµćŗóĮ½Ī»£©.
µÄ½į¹ū¾«Č·µ½Š”ŹżµćŗóĮ½Ī»£©.
”¾“š°ø”æ£Ø1£©¼ū½āĪö£Ø2£©![]() £¬
£¬![]() .
.
”¾½āĪö”æ
£Ø1£©·Ö±š¼ĘĖćĆæ×éµÄʵĀŹ/×é¾ą¼“æÉ£»
£Ø2£©ÓÉĢāŅā¼°ŅŃÖŖæɵĆ![]() £¬×¢Ņāµ½ÖŠ¼äČż×éµÄøÅĀŹŗĶĪŖ0.7£¬ĖłŅŌ
£¬×¢Ņāµ½ÖŠ¼äČż×éµÄøÅĀŹŗĶĪŖ0.7£¬ĖłŅŌ![]() £¬
£¬![]() »ņ
»ņ![]() £¬
£¬![]() £¬·Ö±šĢÖĀŪ¼ĘĖć¼“æɵƵ½“š°ø.
£¬·Ö±šĢÖĀŪ¼ĘĖć¼“æɵƵ½“š°ø.
£Ø1£©øł¾ŻŅŌÉĻŹż¾Ż£¬Ēó³öø÷¶ĪµÄʵĀŹ£¬»ęÖĘ³öʵĀŹ·Ö²¼Ö±·½Ķ¼ČēĻĀ

£Ø2£©”ą![]()
ŅņĪŖµŚ3£¬4£¬5×éµÄøÅĀŹŗĶĪŖ![]() £¬
£¬
ĖłŅŌŅŖŹ¹![]() £¬
£¬
Ōņ![]() £¬
£¬![]() »ņ
»ņ![]() £¬
£¬![]() £¬
£¬
Čō![]() £¬
£¬![]() £¬
£¬
¼“![]()
ÕūĄķµĆ£ŗ![]()
¼“£ŗ![]() £¬ĖłŅŌ
£¬ĖłŅŌ![]()
²»Āś×ć![]() £¬ÉįČ„£»
£¬ÉįČ„£»
Čō![]() £¬
£¬![]() £¬
£¬
ŌņÓŠ![]()
ÕūĄķµĆ£ŗ![]() £¬
£¬![]() Āś×ćĢõ¼ž
Āś×ćĢõ¼ž
¹Ź![]() .
.


 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹżf £Øx£©=ax©ex£Øa”ŹR£©£¬g£Øx£©=![]() £®
£®
£Ø¢ń£©ĒóŗÆŹżf £Øx£©µÄµ„µ÷Ēų¼ä£»
£Ø¢ņ£©x0”Ź£Ø0£¬+”Ž£©£¬Ź¹²»µČŹ½f £Øx£©”Üg£Øx£©©ex³ÉĮ¢£¬ĒóaµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚÖ±½Ē×ų±źĻµxOyÖŠ£¬ĒśĻßC1µÄ²ĪŹż·½³ĢĪŖ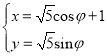 £Ø¦ÕĪŖ²ĪŹż£©£¬ŅŌ×ų±źŌµćOĪŖ¼«µć£¬xÖįµÄÕż°ėÖįĪŖ¼«Öį£¬½ØĮ¢¼«×ų±źĻµ£®
£Ø¦ÕĪŖ²ĪŹż£©£¬ŅŌ×ų±źŌµćOĪŖ¼«µć£¬xÖįµÄÕż°ėÖįĪŖ¼«Öį£¬½ØĮ¢¼«×ų±źĻµ£®
£Ø1£©ĒóC1µÄ¼«×ų±ź·½³Ģ£»
£Ø2£©ČōC1ÓėĒśĻßC2£ŗ¦Ń£½2sin¦Č½»ÓŚA£¬BĮ½µć£¬Ēó|OA||OB|µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÉ菿ĮŠ![]() £ØČĪŅāĻī¶¼²»ĪŖĮć£©µÄĒ°
£ØČĪŅāĻī¶¼²»ĪŖĮć£©µÄĒ°![]() ĻīŗĶĪŖ
ĻīŗĶĪŖ![]() £¬Ź×ĻīĪŖ
£¬Ź×ĻīĪŖ![]() £¬¶ŌÓŚČĪŅā
£¬¶ŌÓŚČĪŅā![]() £¬Āś×ć
£¬Āś×ć![]() .
.
£Ø1£©ŹżĮŠ![]() µÄĶØĻī¹«Ź½£»
µÄĶØĻī¹«Ź½£»
£Ø2£©ŹĒ·ń“ęŌŚ![]() Ź¹µĆ
Ź¹µĆ![]() ³ÉµČ±ČŹżĮŠ£¬ĒŅ
³ÉµČ±ČŹżĮŠ£¬ĒŅ![]() ³ÉµČ²īŹżĮŠ£æČō“ęŌŚ£¬ŹŌĒó
³ÉµČ²īŹżĮŠ£æČō“ęŌŚ£¬ŹŌĒó![]() µÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
µÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø3£©É菿ĮŠ![]() £¬
£¬ £¬ČōÓÉ
£¬ČōÓÉ![]() µÄĒ°
µÄĒ°![]() ĻīŅĄ“Ī¹¹³ÉµÄŹżĮŠŹĒµ„µ÷µŻŌöŹżĮŠ£¬ĒóÕżÕūŹż
ĻīŅĄ“Ī¹¹³ÉµÄŹżĮŠŹĒµ„µ÷µŻŌöŹżĮŠ£¬ĒóÕżÕūŹż![]() µÄ×ī“óÖµ.
µÄ×ī“óÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĖ«Ź®Ņ»¹ŗĪļæń»¶½Ś£¬ŹĒÖøĆæÄź11ŌĀ11ČÕµÄĶųĀē“ŁĻśČÕ£¬Ō“ÓŚĢŌ±¦ÉĢ³Ē(ĢģĆØ)2009Äź11ŌĀ11ČÕ¾Ł°ģµÄĶųĀē“ŁĻś»ī¶Æ£¬ŅŃ³ÉĪŖÖŠ¹śµē×ÓÉĢĪńŠŠŅµµÄÄź¶ČŹ¢ŹĀ.Ä³Éś²śÉĢĪŖĮĖĮĖ½āĘäÉś²śµÄ²śĘ·ŌŚ²»Ķ¬µēÉĢĘ½ĢصÄĻśŹŪĒéæö£¬Ķ³¼ĘĮĖ![]() Į½øöµēÉĢĘ½ĢØø÷Ź®øöĶųĀēĻśŹŪµźĘĢµÄĻśŹŪŹż¾Ż£ŗ
Į½øöµēÉĢĘ½ĢØø÷Ź®øöĶųĀēĻśŹŪµźĘĢµÄĻśŹŪŹż¾Ż£ŗ
| 64 | 71 | 81 | 70 | 79 | 69 | 82 | 73 | 75 | 60 |
| 60 | 80 | 97 | 77 | 96 | 87 | 76 | 83 | 94 | 96 |
£Ø1£©×÷³ö![]() Į½øöµēÉĢĘ½ĢØĻśŹŪŹż¾ŻµÄ¾„Ņ¶Ķ¼£¬øł¾Ż¾„Ņ¶Ķ¼ÅŠ¶ĻÄÄøöµēÉĢĘ½ĢصÄĻśŹŪøüŗĆ£¬²¢ĖµĆ÷ĄķÓÉ£»
Į½øöµēÉĢĘ½ĢØĻśŹŪŹż¾ŻµÄ¾„Ņ¶Ķ¼£¬øł¾Ż¾„Ņ¶Ķ¼ÅŠ¶ĻÄÄøöµēÉĢĘ½ĢصÄĻśŹŪøüŗĆ£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø2£©ĢīŠ“ĻĀĆę¹ŲÓŚµźĘĢøöŹżµÄ![]() ĮŠĮŖ±ķ£¬²¢øł¾ŻĮŠĮŖ±ķÅŠ¶ĻŹĒ·ńÓŠ
ĮŠĮŖ±ķ£¬²¢øł¾ŻĮŠĮŖ±ķÅŠ¶ĻŹĒ·ńÓŠ![]() µÄ°ŃĪÕČĻĪŖĻśŹŪĮæÓėµēÉĢĘ½ĢØÓŠ¹Ų£»
µÄ°ŃĪÕČĻĪŖĻśŹŪĮæÓėµēÉĢĘ½ĢØÓŠ¹Ų£»
ĻśŹŪĮæ | ĻśŹŪĮæ | ×Ü¼Ę | |
| |||
| |||
×Ü¼Ę |
£Ø3£©Éś²śÉĢŅŖ“ÓÕā20øöĶųĀēĻśŹŪµźĘĢĻśŹŪĮæĒ°ĪåĆūµÄµźĘĢÖŠ£¬Ė껜³éȔȿøöµźĘĢ½ųŠŠĻśŹŪ·µĄū£¬ŌņĘäÖŠĒ”ŗĆÓŠĮ½øöµźĘĢµÄĻśŹŪĮæŌŚ95ŅŌÉĻµÄøÅĀŹŹĒ¶ąÉŁ£æ
ø½£ŗ £¬
£¬![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖĶÖŌ²C£ŗ![]() µÄ×ó”¢ÓŅ¶„µć·Ö±šĪŖ
µÄ×ó”¢ÓŅ¶„µć·Ö±šĪŖ![]() ÓŅ½¹µćĪŖ
ÓŅ½¹µćĪŖ![]() £¬ÓŅ×¼ĻßlµÄ·½³ĢĪŖ
£¬ÓŅ×¼ĻßlµÄ·½³ĢĪŖ![]() £¬¹ż½¹µćFµÄÖ±ĻßÓėĶÖŌ²CĻą½»ÓŚµćA£¬B£Ø²»Óėµć
£¬¹ż½¹µćFµÄÖ±ĻßÓėĶÖŌ²CĻą½»ÓŚµćA£¬B£Ø²»Óėµć![]() ÖŲŗĻ£©.
ÖŲŗĻ£©.
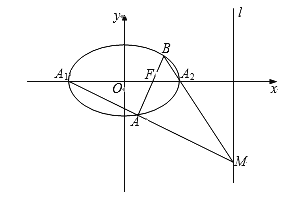
£Ø1£©ĒóĶÖŌ²CµÄ±ź×¼·½³Ģ£»
£Ø2£©µ±Ö±ĻßABµÄĒ抱½ĒĪŖ45”揱£¬ĒóĻŅABµÄ³¤£»
£Ø3£©ÉčÖ±Ļß![]() ½»lÓŚµćM£¬ĒóÖ¤£ŗB£¬
½»lÓŚµćM£¬ĒóÖ¤£ŗB£¬![]() £¬MČżµć¹²Ļß.
£¬MČżµć¹²Ļß.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĖÄĄā׶![]() ÖŠ£¬
ÖŠ£¬![]() ŹĒµČ±ßČż½ĒŠĪ£¬
ŹĒµČ±ßČż½ĒŠĪ£¬![]() £¬
£¬![]() £¬
£¬![]() .
.
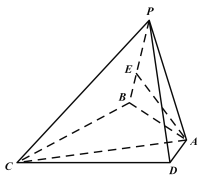
£Ø1£©Čō![]() £¬ĒóČżĄā׶
£¬ĒóČżĄā׶![]() µÄĢå»ż£»
µÄĢå»ż£»
£Ø2£©Čō![]() £¬ŌņŌŚĻ߶Ī
£¬ŌņŌŚĻ߶Ī![]() ÉĻŹĒ·ń“ęŌŚŅ»µć
ÉĻŹĒ·ń“ęŌŚŅ»µć![]() £¬Ź¹Ę½Ćę
£¬Ź¹Ę½Ćę![]() Ę½Ćę
Ę½Ćę![]() .Čō“ęŌŚ£¬ĒóĻ߶Ī
.Čō“ęŌŚ£¬ĒóĻ߶Ī![]() µÄ³¤£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
µÄ³¤£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĮ½øöŹżĮŠ![]() ”¢
”¢![]() £¬µ±
£¬µ±![]() ŗĶ
ŗĶ![]() Ķ¬Ź±ŌŚ
Ķ¬Ź±ŌŚ![]() Ź±Č”µĆĻąĶ¬µÄ×ī“óÖµ£¬ĪŅĆĒ³Ę
Ź±Č”µĆĻąĶ¬µÄ×ī“óÖµ£¬ĪŅĆĒ³Ę![]() Óė
Óė![]() ¾ßÓŠŠŌÖŹ
¾ßÓŠŠŌÖŹ![]() £¬ĘäÖŠ
£¬ĘäÖŠ![]() .
.
£Ø1£©Éč![]() µÄ¶žĻīÕ¹æŖŹ½ÖŠ
µÄ¶žĻīÕ¹æŖŹ½ÖŠ![]() µÄĻµŹżĪŖ
µÄĻµŹżĪŖ![]() £Ø
£Ø![]() £©£¬
£©£¬![]() £¬¼Ē
£¬¼Ē![]() £¬
£¬![]() £¬
£¬![]() £¬ŅĄ“ĪĻĀČ„£¬
£¬ŅĄ“ĪĻĀČ„£¬![]() £¬×é³ÉµÄŹżĮŠŹĒ
£¬×é³ÉµÄŹżĮŠŹĒ![]() £»Ķ¬ŃłµŲ£¬
£»Ķ¬ŃłµŲ£¬![]() µÄ¶žĻīÕ¹æŖŹ½ÖŠ
µÄ¶žĻīÕ¹æŖŹ½ÖŠ![]() µÄĻµŹżĪŖ
µÄĻµŹżĪŖ![]() £Ø
£Ø![]() £©£¬
£©£¬![]() £¬¼Ē
£¬¼Ē![]() £¬
£¬![]() £¬
£¬![]() £¬ŅĄ“ĪĻĀČ„£¬
£¬ŅĄ“ĪĻĀČ„£¬![]() £¬×é³ÉµÄŹżĮŠŹĒ
£¬×é³ÉµÄŹżĮŠŹĒ![]() £»ÅŠ±š
£»ÅŠ±š![]() Óė
Óė![]() ŹĒ·ń¾ßÓŠŠŌÖŹ
ŹĒ·ń¾ßÓŠŠŌÖŹ![]() £¬ĒėĖµĆ÷ĄķÓÉ£»
£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø2£©ŹżĮŠ![]() µÄĒ°
µÄĒ°![]() ĻīŗĶŹĒ
ĻīŗĶŹĒ![]() £¬ŹżĮŠ
£¬ŹżĮŠ![]() µÄĒ°
µÄĒ°![]() ĻīŗĶŹĒ
ĻīŗĶŹĒ![]() £¬Čō
£¬Čō![]() Óė
Óė![]() ¾ßÓŠŠŌÖŹ
¾ßÓŠŠŌÖŹ![]() £¬
£¬![]() £¬ŌņÕāŃłµÄŹżĮŠ
£¬ŌņÕāŃłµÄŹżĮŠ![]() Ņ»¹²ÓŠ¶ąÉŁøö£æĒėĖµĆ÷ĄķÓÉ£»
Ņ»¹²ÓŠ¶ąÉŁøö£æĒėĖµĆ÷ĄķÓÉ£»
£Ø3£©Į½øöÓŠĻŽĻīŹżĮŠ![]() Óė
Óė![]() Āś×ć
Āś×ć![]() £¬
£¬![]() £¬ĒŅ
£¬ĒŅ![]() £¬ŹĒ·ń“ęŌŚŹµŹż
£¬ŹĒ·ń“ęŌŚŹµŹż![]() £¬Ź¹µĆ
£¬Ź¹µĆ![]() Óė
Óė![]() ¾ßÓŠŠŌÖŹ
¾ßÓŠŠŌÖŹ![]() £¬ĒėĖµĆ÷ĄķÓÉ.
£¬ĒėĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij¹«Ė¾ÅąŃµŌ±¹¤Ä³Ļī¼¼ÄÜ£¬ÅąŃµÓŠČēĻĀĮ½ÖÖ·½Ź½£ŗ
·½Ź½Ņ»£ŗÖÜŅ»µ½ÖÜĪåĆæĢģÅąŃµ1Š”Ź±£¬ÖÜČÕ²āŹŌ
·½Ź½¶ž£ŗÖÜĮłŅ»ĢģÅąŃµ4Š”Ź±£¬ÖÜČÕ²āŹŌ
¹«Ė¾ÓŠ¶ąøö°ą×飬Ćæøö°ą×é60ČĖ£¬ĻÖČĪŃ”Į½×é![]() ¼ĒĪŖ¼××锢ŅŅ×é
¼ĒĪŖ¼××锢ŅŅ×é![]() ĻČÅąŃµ£»¼××éŃ”·½Ź½Ņ»£¬ŅŅ×éŃ”·½Ź½¶ž£¬²¢¼ĒĀ¼ĆæÖÜÅąŃµŗó²āŹŌ“ļ±źµÄČĖŹżČē±ķ£ŗ
ĻČÅąŃµ£»¼××éŃ”·½Ź½Ņ»£¬ŅŅ×éŃ”·½Ź½¶ž£¬²¢¼ĒĀ¼ĆæÖÜÅąŃµŗó²āŹŌ“ļ±źµÄČĖŹżČē±ķ£ŗ
µŚŅ»ÖÜ | µŚ¶žÖÜ | µŚČżÖÜ | µŚĖÄÖÜ | |
¼××é | 20 | 25 | 10 | 5 |
ŅŅ×é | 8 | 16 | 20 | 16 |
![]() ÓĆ·½Ź½Ņ»Óė·½Ź½¶ž½ųŠŠÅąŃµ£¬·Ö±š¹Ą¼ĘŌ±¹¤ŹÜѵµÄĘ½¾łŹ±¼ä
ÓĆ·½Ź½Ņ»Óė·½Ź½¶ž½ųŠŠÅąŃµ£¬·Ö±š¹Ą¼ĘŌ±¹¤ŹÜѵµÄĘ½¾łŹ±¼ä![]() ¾«Č·µ½
¾«Č·µ½![]() £¬²¢¾Ż“ĖÅŠ¶ĻÄÄÖÖÅąŃµ·½Ź½Š§ĀŹøüøߣæ
£¬²¢¾Ż“ĖÅŠ¶ĻÄÄÖÖÅąŃµ·½Ź½Š§ĀŹøüøߣæ
![]() ŌŚ¼×ŅŅĮ½×éÖŠ£¬“ÓµŚČżÖÜÅąŃµŗó“ļ±źµÄŌ±¹¤ÖŠ²ÉÓĆ·Ö²ć³éŃłµÄ·½·Ø³éČ”6ČĖ£¬ŌŁ“ÓÕā6ČĖÖŠĖ껜³éČ”2ČĖ£¬ĒóÕā2ČĖÖŠÖĮÉŁÓŠ1ČĖĄ“×Ō¼××éµÄøÅĀŹ£®
ŌŚ¼×ŅŅĮ½×éÖŠ£¬“ÓµŚČżÖÜÅąŃµŗó“ļ±źµÄŌ±¹¤ÖŠ²ÉÓĆ·Ö²ć³éŃłµÄ·½·Ø³éČ”6ČĖ£¬ŌŁ“ÓÕā6ČĖÖŠĖ껜³éČ”2ČĖ£¬ĒóÕā2ČĖÖŠÖĮÉŁÓŠ1ČĖĄ“×Ō¼××éµÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com