
【题目】已知函数f (x)=ax﹣ex(a∈R),g(x)=![]() .
.
(Ⅰ)求函数f (x)的单调区间;
(Ⅱ)x0∈(0,+∞),使不等式f (x)≤g(x)﹣ex成立,求a的取值范围.
【答案】(Ⅰ)答案见解析(Ⅱ)![]()
【解析】
试题(Ⅰ)f′(x)=a﹣ex,x∈R.对a分类讨论,利用导数研究函数的单调性即可得出;
(Ⅱ)由x0∈(0,+∞),使不等式f(x)≤g(x)﹣ex,即a≤![]() .设h(x)=
.设h(x)=![]() ,则问题转化为a
,则问题转化为a![]() ,利用导数研究函数的单调性极值与最值即可得出.
,利用导数研究函数的单调性极值与最值即可得出.
解:(Ⅰ)∵f′(x)=a﹣ex,x∈R.
当a≤0时,f′(x)<0,f(x)在R上单调递减;
当a>0时,令f′(x)=0得x=lna.
由f′(x)>0得f(x)的单调递增区间为(﹣∞,lna);
由f′(x)<0得f(x)的单调递减区间为(lna,+∞).
(Ⅱ)∵x0∈(0,+∞),使不等式f(x)≤g(x)﹣ex,则![]() ,即a≤
,即a≤![]() .
.
设h(x)=![]() ,则问题转化为a
,则问题转化为a![]() ,
,
由h′(x)=![]() ,令h′(x)=0,则x=
,令h′(x)=0,则x=![]() .
.
当x在区间(0,+∞) 内变化时,h′(x)、h(x)变化情况如下表:

由上表可知,当x=![]() 时,函数h(x)有极大值,即最大值为
时,函数h(x)有极大值,即最大值为![]() .
.
∴![]() .
.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】某商场春节期间推出一项优惠活动,活动规则如下:消费额每满300元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在区域Ⅰ返券60元;停在区域Ⅱ返券30元;停在区域Ⅲ不返券.例如:消费600元,可抽奖2次,所获得的返券金额是两次金额之和.
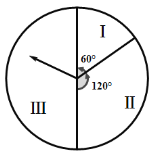
(Ⅰ)若某位顾客消费300元,求返券金额不低于30元的概率;
(Ⅱ)若某位顾客恰好消费600元,并按规则参与了活动,他获得返券的金额记为![]() (元).求随机变量
(元).求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有一个“引葭赴岸”问题:“今有池方一丈,葭生其中央.出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?”其意思为“今有水池1丈见方(即![]() 尺),芦苇生长在水的中央,长出水面的部分为1尺.将芦苇向池岸牵引,恰巧与水岸齐接(如图所示).试问水深、芦苇的长度各是多少?假设
尺),芦苇生长在水的中央,长出水面的部分为1尺.将芦苇向池岸牵引,恰巧与水岸齐接(如图所示).试问水深、芦苇的长度各是多少?假设![]() ,现有下述四个结论:
,现有下述四个结论:
①水深为12尺;②芦苇长为15尺;③![]() ;④
;④![]() .
.
其中所有正确结论的编号是( )

A.①③B.①③④C.①④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】医院为筛查某种疾病,需要血检,现有![]() 份血液样本,有以下两种检验方式:
份血液样本,有以下两种检验方式:
方式一:逐份检验,需要检验![]() 次;
次;
方式二:混合检验,把每个人的血样分成两份,取![]() 个人的血样各一份混在一起进行检验,如果结果是阴性,那么对这
个人的血样各一份混在一起进行检验,如果结果是阴性,那么对这![]() 个人只作一次检验就够了;如果结果是阳性,那么再对这
个人只作一次检验就够了;如果结果是阳性,那么再对这![]() 个人的另一份血样逐份检验,此时这
个人的另一份血样逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() 次.
次.
(1)假设有6份血液样本,其中只有2份样本为阳性,若采用逐份检验的方式,求恰好经过3次检验就能把阳性样本全部检验岀来的概率;
(2)假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是相互独立的,且每份样本是阳性结果的概率为![]() .现取其中
.现取其中![]() (
(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
①运用概率统计的知识,若![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
②若![]() ,且采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求
,且采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求![]() 的最大值.
的最大值.
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 、抛物线
、抛物线![]() 的焦点均在
的焦点均在![]() 轴上,
轴上,![]() 的中心和
的中心和![]() 的顶点均为原点
的顶点均为原点![]() ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
| 3 |
| 4 |
|
|
| 0 |
|
|
(Ⅰ)求![]() 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线![]() 满足条件:①过
满足条件:①过![]() 的焦点
的焦点![]() ;②与
;②与![]() 交不同两点
交不同两点![]() 且满足
且满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年电子商务蓬勃发展,现从某电子商务平台评价系统中随机选出200次成功交易,并对其评价进行统计,统计结果显示:网购者对商品的满意率为0.70,对快递的满意率为0.60,其中对商品和快递都满意的交易为80次.
(1)根据已知条件完成下面的2×2列联表,并回答在犯错误的概率不超过0.10的前提下,能否认为“网购者对商品满意与对快递满意之间有关系”?
对快递满意 | 对快递不满意 | 合计 | |
对商品满意 | 80 | ||
对商品不满意 | |||
合计 | 200 |
(2)为进一步提高购物者的满意度,平台按分层抽样方法从200次交易中抽取10次交易进行问卷调查,详细了解满意与否的具体原因,并在这10次交易中再随机抽取2次进行电话回访,听取购物者意见.求电话回访的2次交易至少有一次对商品和快递都满意的概率.
附: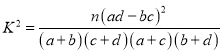 (其中
(其中![]() 为样本容量)
为样本容量)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】跨年迎新联欢晚会简称跨年晚会,是指每年阳历年末12月31日晚上各电视台和政府为喜迎新而精心策划的演唱会活动,跨年晚会首次出现在港台地区,跨年晚会因形式和举办地不同因而名称也不同,如央视启航2020跨年盛典,湖南卫视跨年演唱会,东方卫视迎新晚会等.某电视台为了了解2020年举办的跨年迎新晚会观众的满意度,现分别随机选出![]() 名观众对迎新晚会的质量评估评分,最高分为
名观众对迎新晚会的质量评估评分,最高分为![]() 分,综合得分情况如下表所示:
分,综合得分情况如下表所示:
综合得分 |
|
|
|
|
|
|
|
观众人数 | 5 | 10 | 25 | 30 | 15 | 10 | 5 |
根据表中的数据,回答下列问题:
(1)根据表中的数据,绘制这![]() 位观众打分的频率分布直方图;
位观众打分的频率分布直方图;
(2)已知观众的评分![]() 近似服从
近似服从![]() ,其中
,其中![]() 是反应随机变量
是反应随机变量![]() 取值的平均水平的特征数,工作人员在分析数据时发现,可用
取值的平均水平的特征数,工作人员在分析数据时发现,可用![]() 位观众评分的平均数估计
位观众评分的平均数估计![]() ,但由于评分观众人数较少,误差较大,所以不能直接用
,但由于评分观众人数较少,误差较大,所以不能直接用![]() 位观众评分的标准差的值估计
位观众评分的标准差的值估计![]() ,而在这
,而在这![]() 位观众打分的频率分布直方图的基础上依据
位观众打分的频率分布直方图的基础上依据![]() 来估计
来估计![]() 更科学合理,试求
更科学合理,试求![]() 和
和![]() 的估计值(
的估计值(![]() 的结果精确到小数点后两位).
的结果精确到小数点后两位).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com